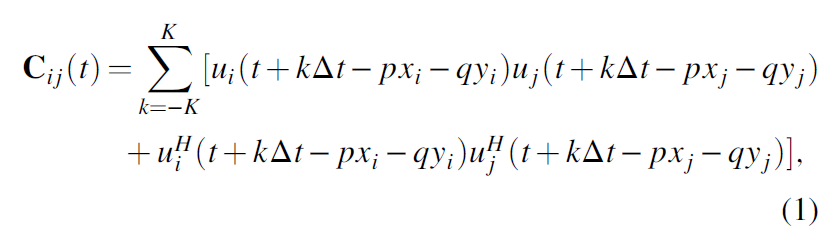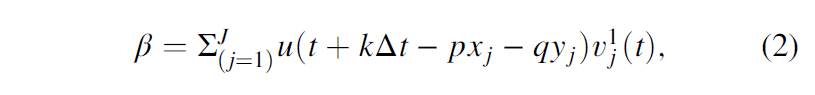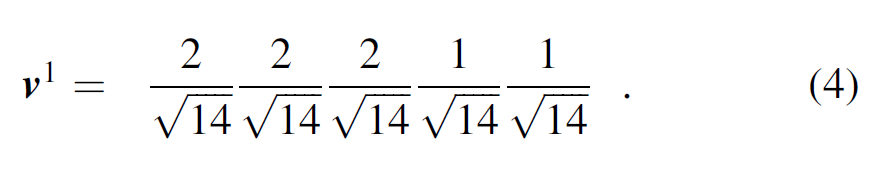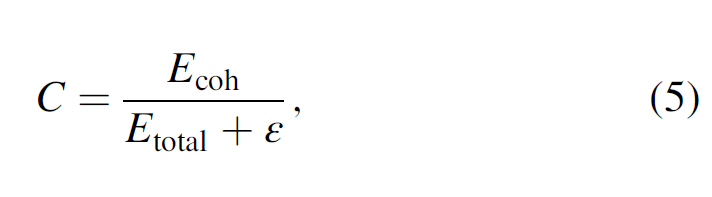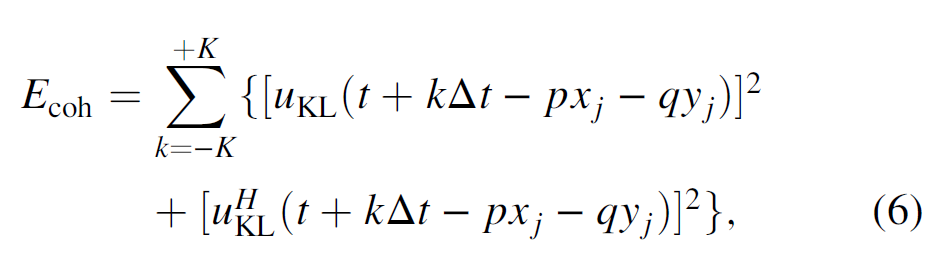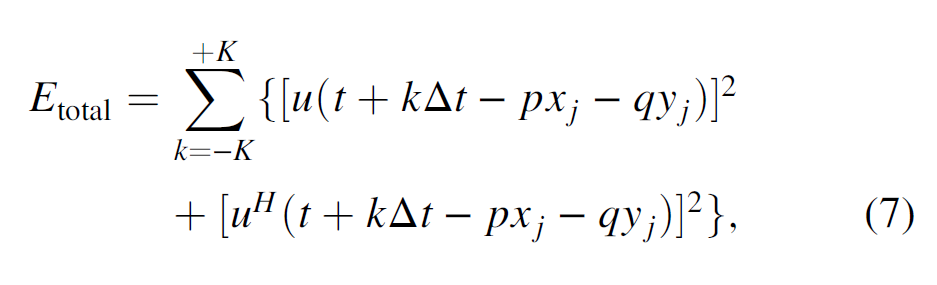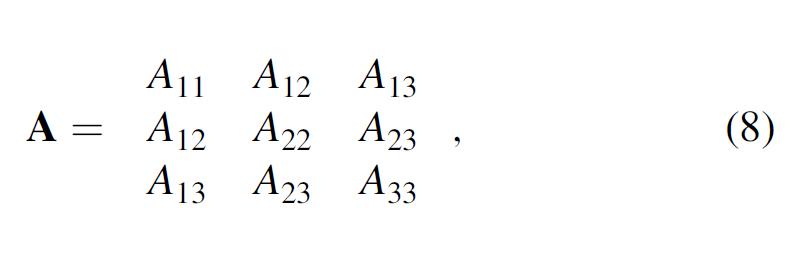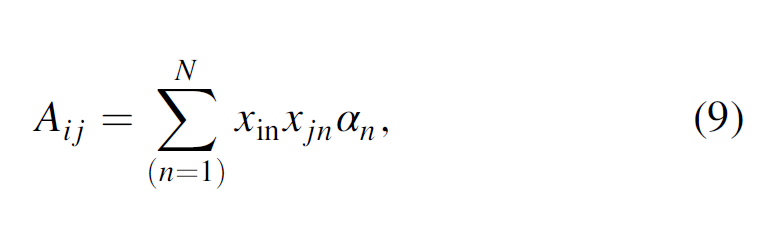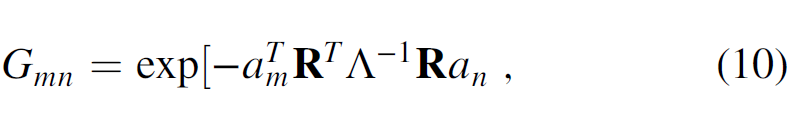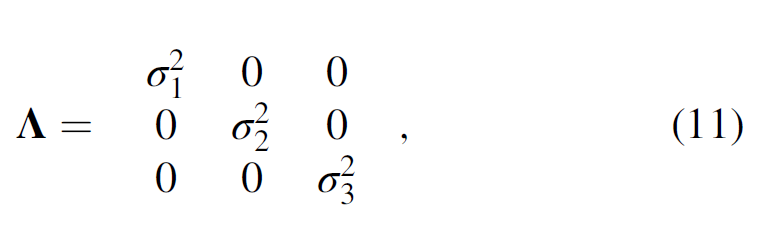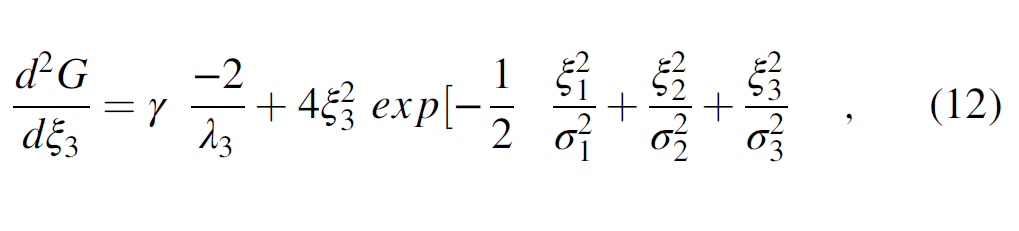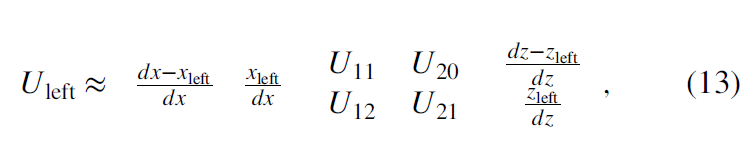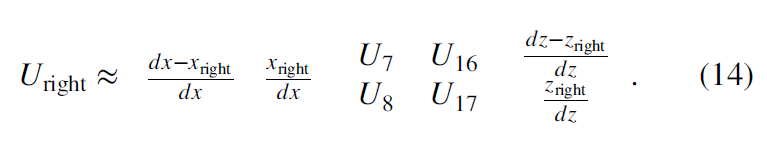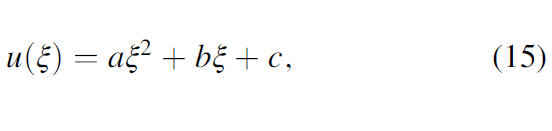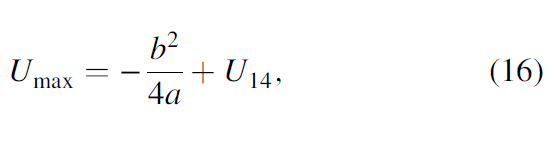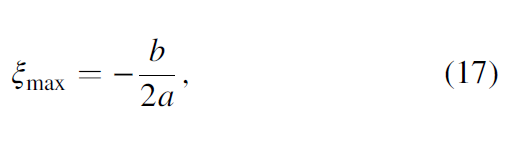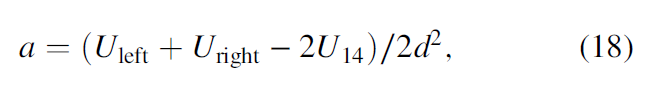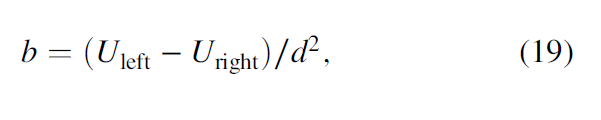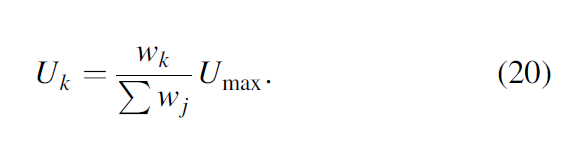By Jie Qi, Gabriel Machado, and Kurt Marfurt | Published with permission: Geophysics Vol. 82, No. 4 | July 2017
Abstract
Improving the accuracy and completeness of subtle discontinuities in noisy seismic data is useful for mapping faults, fractures, unconformities, and stratigraphic edges. We have developed a workflow to improve the quality of coherence attributes. First, we apply principal component structure-oriented filtering to reject random noise and sharpen the lateral edges of seismic amplitude data. Next, we compute eigenstructure coherence, which highlights the stratigraphic and structural discontinuities. We apply a Laplacian of a Gaussian filter to the coherence attribute that sharpens the steeply dipping faults, attenuates the stratigraphic features parallel to the seismic reflectors, and skeletonizes the unconformity features subparallel to the reflectors. Finally, we skeletonize the filtered coherence attribute along with the fault plane. The filtered and skeletonized seismic coherence attribute highlights the geologic discontinuities more clearly and precisely. These discontinuous features can be color coded by their dipping orientation or as a suite of independent, azimuthally limited volumes, providing the interpreter a means of isolating fault sets that are either problematic or especially productive. We validate the effectiveness of our workflow by applying it to seismic surveys acquired from the Gulf of Mexico, USA, and the Great South Basin, New Zealand. The skeletonized result rejects noise and enhances discontinuities seen in the vertical and lateral directions. The corendering of the “fault” azimuth and the fault-dip magnitude exhibits the strengths of the discontinuities and their orientation. Finally, we compared our workflow with the results generated from the swarm intelligence and found our method to be better at tracking short faults and stratigraphic discontinuities.
Introduction
Identification and mapping faults is one of the most important steps in seismic data interpretation in conventional plays, whereas fault identification is critical for identifying potential drilling hazards and characterizing natural fractures in unconventional resource plays. Although major faults seen in a seismic amplitude volume can be easily identified and picked by experienced interpreters, the process is still time consuming, particularly in picking more subtle faults masked by noise. A huge effort has been made to accelerate the procedure of seismic interpretation. In this paper, we introduce a 3D workflow that minimizes coherence artifacts, links disconnected faults and stratigraphic edges, and skeletonizes the results.
Coherence (Marfurt et al., 1998; Gersztenkorn and Marfurt, 1999) is routinely used to detect structural discontinuities in 3D seismic data. Other edge-detection algorithms (e.g., Luo et al.,1996; Dorn et al., 2012; Wang et al., 2016) provide similar results. Unfortunately, coherence measures all lateral discontinuities, including where steeply dipping coherent noise interferes with more gently dipping reflectors. Coherence also delineates channel edges, carbonate buildups, slumps, collapse features, and angular unconformities. In addition, coherence can also be used to detect chaotic textures in multiattribute seismic facies analysis (Qi et al., 2016). Automatic fault extraction in most commercial software packages requires that the seismic attribute is first smoothed prior to skeletonization. Seismic data conditioning for fault interpretation includes removing incoherent noise, sharpening the edges between the hanging wall and footwall, and flattening the spectrum of the seismic data. Fehmers and Höcher (2003) propose an edge-preserving structure-oriented filtering (SOF) workflow that uses anisotropic diffusion to reject crosscutting noise in 3D seismic data. Marfurt (2006) generalizes an algorithm developed by Luo (2002), based on overlapping Kuwahara windows. Davogustto and Marfurt (2011) combine these two approaches into one algorithm and cascade them with kx-ky footprint suppression. Zhang et al. (2015) apply the SOF workflow to prestack time-migrated data that improves prestack seismic inversion results. Spectral balancing also improves the coherence image and partially diminished the stair-step artifacts commonly seen on the vertical slices. All these processes are applied to the seismic amplitude data and can be thought to be seismic data processing.
However, one can also filter the coherence image, which we call “image processing.” One of the more popular algorithms is based on swarm intelligence (Randen et al., 2001; Pedersen et al., 2002). Some automated fault-extraction algorithms need human supervision to select appropriate pilot samples or traces. Other innovations include an edge-detection algorithm described by Zhang et al. (2014) that generates skeletonized fault sticks on time slices. The local fault-extraction method can result in a suite of one- pixel-thick labeled fault surfaces from seismic data (Cohen et al., 2006). Wu and Hale (2015) describe a method that maps intersecting faults based on Hale (2013)’s fault-construction technique. AlBinHassan and Marfurt (2003) and Boe (2012) apply Radon transforms to improve fault images, whereas Kadlec et al. (2008) use level sets to address the same objective. Barnes (2006) constructs a second moment tensor of coherence values falling with an analysis window about each voxel to determine the fault orientation, rejecting anomalies parallel to stratigraphy. He then dilates the images to connect disjointed fault segments, followed by skeletonization to reduce their thickness.
Other 3D attribute-based visualization techniques (Wallet et al., 2011; Qi et al., 2014; Marfurt, 2015; Wu and Hale, 2016) are also useful for fault and discontinuity interpretation. Faults illuminated by different geometric attributes can be corendered using red, green, and blue (RGB) or cyan, magenta, and yelow (CMY) to corender multiple coherence volumes computed from spectral components (Henderson et al., 2008; Li and Lu, 2014). Dewett and Henza (2016) extend this approach beyond these coherence images using self-organizing maps to combine the results. These combined fault images were subsequently enhanced using swarm intelligence.
In this paper, we introduce a 3D fault directional skeletonization workflow (Figure 1) that uses the dip magnitude and azimuth of a directional Laplacian of a Gaussian (LoG) enhanced discontinuities image. We begin our paper by using principal-component SOF to suppress the random and steeply dipping coherent noise on the seismic amplitude data. Then, we compute the coherence attribute from the original and filtered seismic amplitude volumes and compare the results. Next, we apply a directional LoG filter resulting in a smooth but somewhat blurred image. Finally, we skeletonize the LoG filtered image perpendicularly to sharpen the locally planar features.
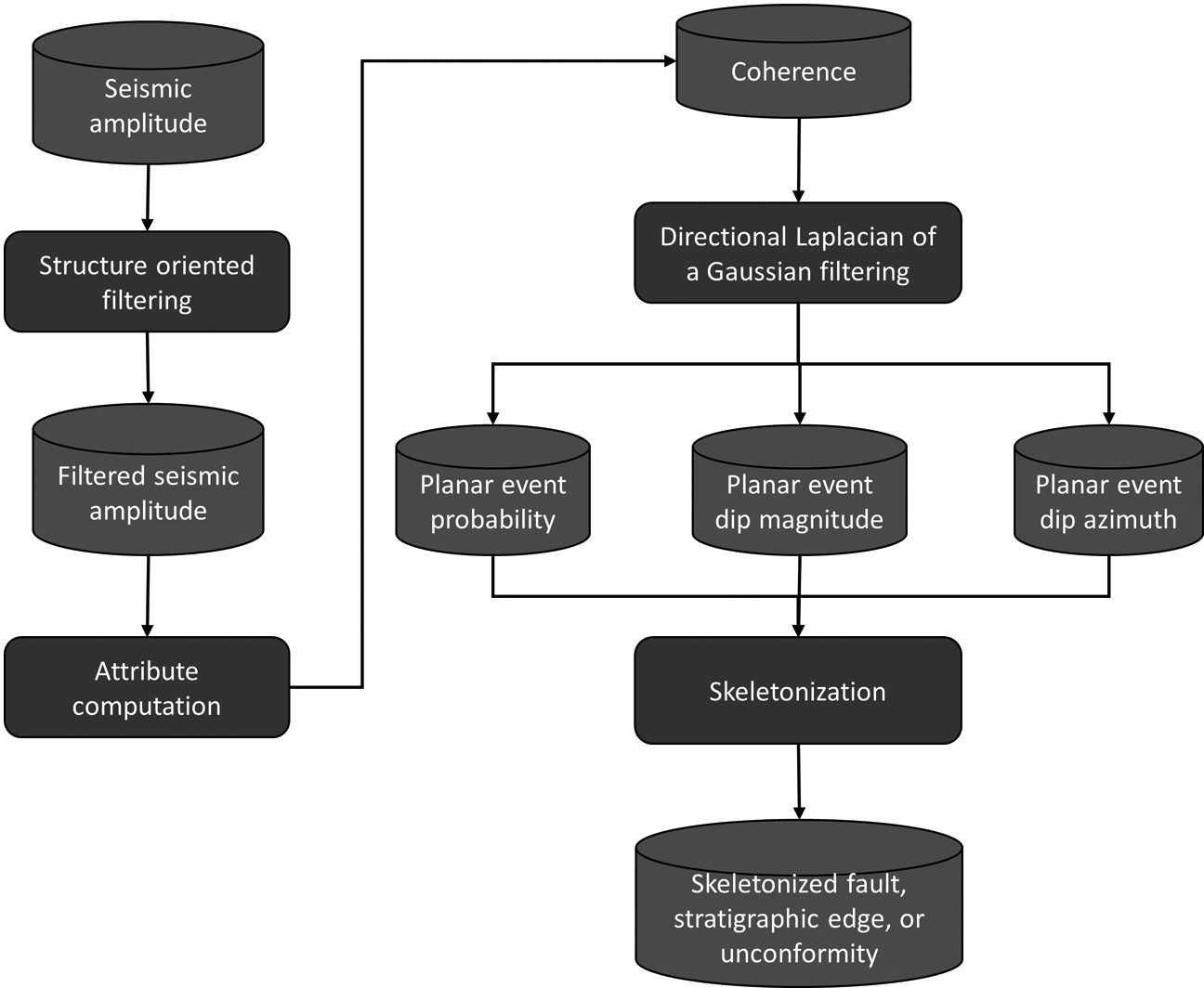
Methods
Poststack data conditioning
Seismic attributes quantify patterns seen among neighboring seismic samples and traces to extract subtle features valuable for interpretation. For this reason, minor improvements of poststack amplitude data can significantly improve subsequent attribute imges. In this workflow, we use a Karhunen-Loève (principal-component) filter aligned with a structure to suppress random and any crosscutting coherent noise. Each voxel has an estimate of coherence. Of all the overlapping windows that contain our analysis point, we choose the window that is most coherent (Davogustto and Marfurt, 2011). Within this window about an analysis point ul at time t, we compute the covariance matrix Cij:
where ui and uj indicate the ith and jth trace, xi and yi (xj and yj) are the distance along the x– and y-axes of the ith (jth) trace from the analysis point, p and q are the apparent dip in the x– and y-direction measured in s∕m, and superscript H denotes the Hilbert transform. The samples along the structural dip for a fixed value of k form what is called a sample vector. The first eigenvector v1 of the matrix C best represents the lateral variation in each of the sample vectors. Crosscorrelating this eigenvector with the sample vector that includes the analysis point gives a crosscorrelation coefficient β:
and the KL-filtered (or first principal component) of the data uKL at time t is then a scaled version of the eigenvector v1:
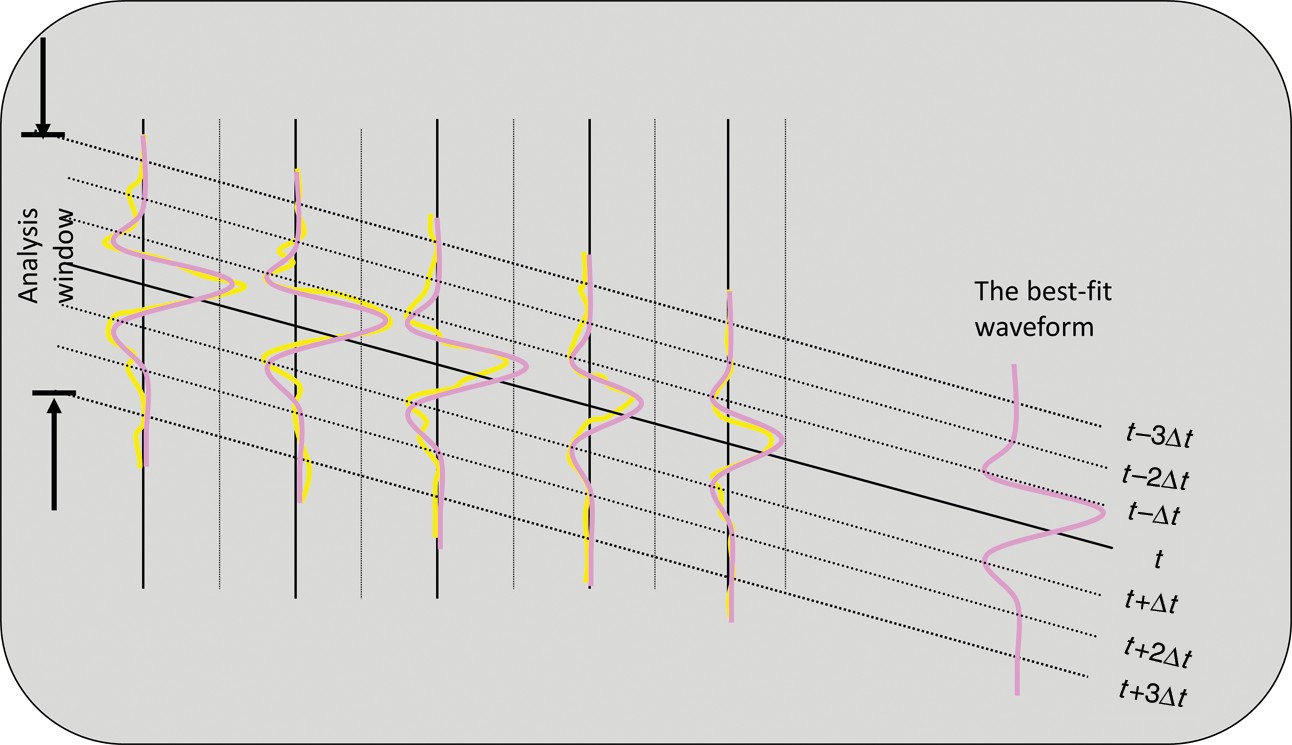
The “Kuwahara” window is in general laterally and vertically not centered about the analysis point ul. An analysis window of five traces and seven interpolated sample vectors, u t kΔt is shown in Figure 2. Note that in this cartoon, the wavelet amplitude of the three leftmost traces is approximately two times larger than that of the two rightmost traces. Each sample vector approximately reflects a scaled version of the pattern (2, 2, 2, 1, 1), where the scaling factor can be positive for a peak, negative for a trough, or zero for a zero crossing. The first eigenvector for this cartoon will be a unit length vector representing this pattern:
Projecting the central sample vector at time t against the eigenvector v1 gives a crosscorrelation coefficient β. For SOF, one scales v1 by β giving the KL-filtered version of the seismic data. Note that because the covariance matrix is used to compute the first eigenvector from seven sample vectors, the statistical analysis involves seven times as much input data as for a simple mean filter. Furthermore, by using the laterally varying eigenvector, one better preserves the lateral change in amplitude in the original data.
Coherence
Coherence is an edge-detection attribute, and it measures lateral changes in the seismic waveform and amplitude. There are several popular coherence algorithms, including those based on semblance (Marfurt et al., 1998), eigenstructure (Gersztenkorn and Marfurt, 1999), the gradient structure tensor method (Bakker et al., 1999), and the Sobel filter (Luo et al., 1996; Luo, 2002). In our workflow, we use an energy ratio coherence of J traces in a K sample analysis window defined as the ratio between the energy of the coherent (KL-filtered data, uKL) to the energy of the unfiltered (or total data, u) within the analysis window centered about the analysis point:
where the coherent energy Ecoh (the energy of the KL-filtered data) is
the total energy Etotal of unfiltered data in the analysis window is
and where a small positive value ε prevents division by zero, and superscript H denotes the Hilbert transform. Application of a Hilbert transform of seismic data avoids unstable estimates of the covariance matrix for small vertical windows centered about a trace zero crossing (Marfurt, 2006). We applied the technique to volumes using a semblance and Sobel-filter algorithm, as well as the energy- ratio coherence algorithm all of which are computed along the structural dip. There is no significant difference for the larger, through-going faults. As expected, small discontinuities that are better delineated by energy-ratio coherence provide greater details. In contrast, if there is a footprint in the coherence images, skeletonization will sharpen it.
Fault enhancement
The goal of fault enhancement is to suppress incoherent noise and enhance faults trends. Although coherence highlights faults and channel edges, these fault images may be broken. A normal fault plane defines the surface between the footwall and the hanging wall (Figure 3). Following Barnes (2006) and Machado et al. (2016), in an N-voxel (αn) spherical analysis window, the second-order mo- ment tensor A of the discontinuity data αnðx1; x2; x3Þ is
where the elements Aij
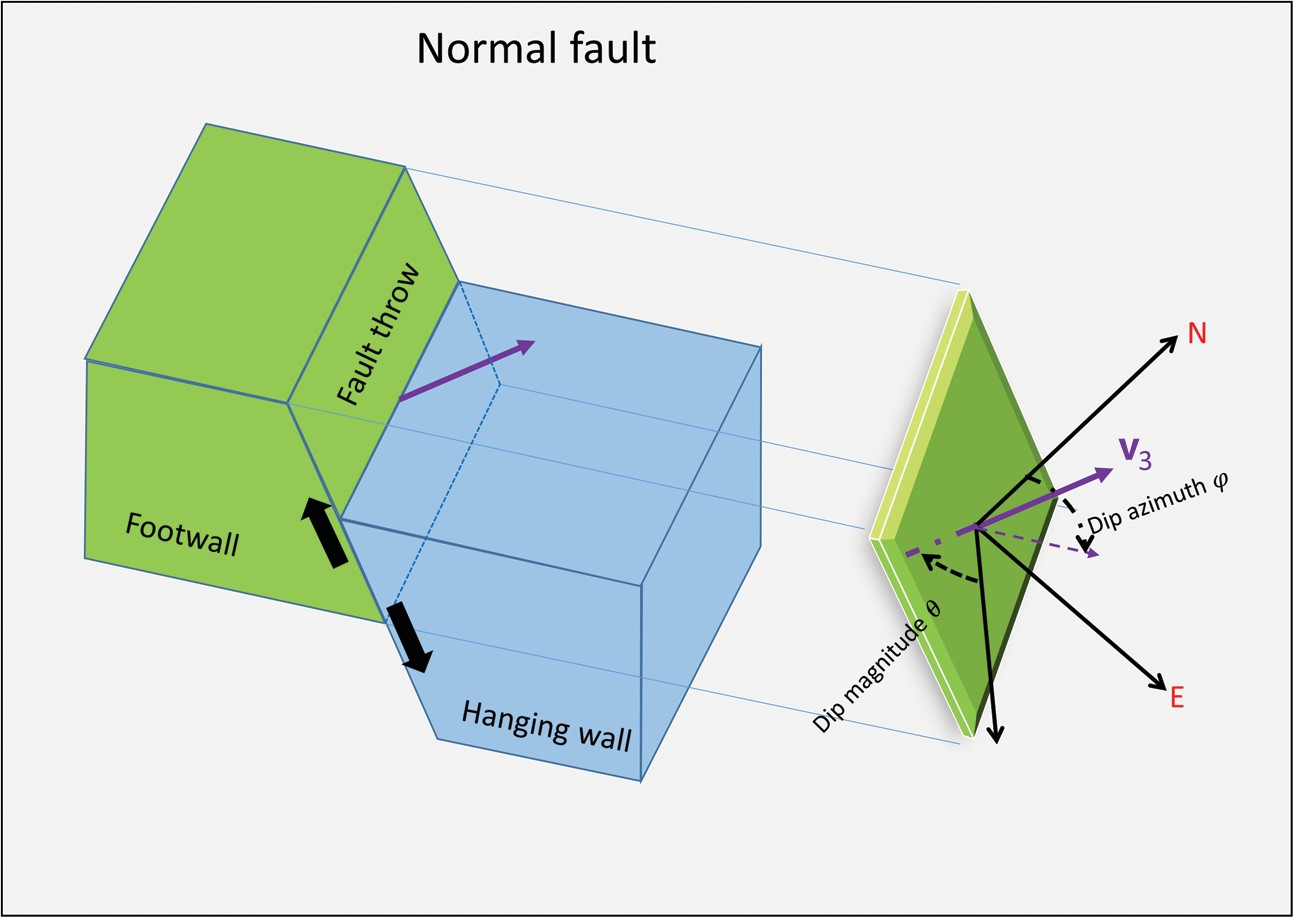
where xin are the distances from the center of the analysis window. If the input coherence data are computed from time-migrated data, z-axis should be stretched to depth. For planar coherence anomalies, the three eigenvalues i of the second moment tensor A will have 1 ≥ 2 ≫ 3. The eigenvectors v1 and v2 of the second-order moment tensor represent the planar surface, whereas the eigenvector v3 represents the normal to the planar surface. The eigenvector v3 has three components with v31 positive to the north, v32 positive to the east, and v33 positive down (Figure 3). Machado et al. (2016) apply a directional LoG operator to 3D seismic data to smooth along and sharpen the faults perpendicular to locally planar events. The Gaussian smoother is elongated along the plane (defined by the eigen- vectors v1 and v2)
where R is the rotation matrix and defined as ½ v1 v2 v3 . The function Λ is a diagonal matrix and is defined as
where the value of σ1 and σ2 is three times the bin size, and σ3 is the bin size. The rotation matrix R is aligned with the eigenvector v3. Thus, the second derivative of the Gaussian in the eigenvector v3 direction (ξ3) is
where ξ1, ξ2, and ξ3 are aligned along the eigenvector v1, v2, and v3, respectively, and γ is a normalization factor. Because the directional LoG filter is based on a Gaussian distribution function, we call our filtered result a “fault-probability” image.
Fault skeletonization
Finding eigenvector v3 is the key to directionally skeletonizing planar anomalies in coherence images (Qi et al., 2016). For each voxel, we extract 26 neighboring samples of fault probability that fall within a dx dy dz gridded window (Figure 4). Figure 4a shows a hypothesized plane in green, intersecting the center of the window at point U14.
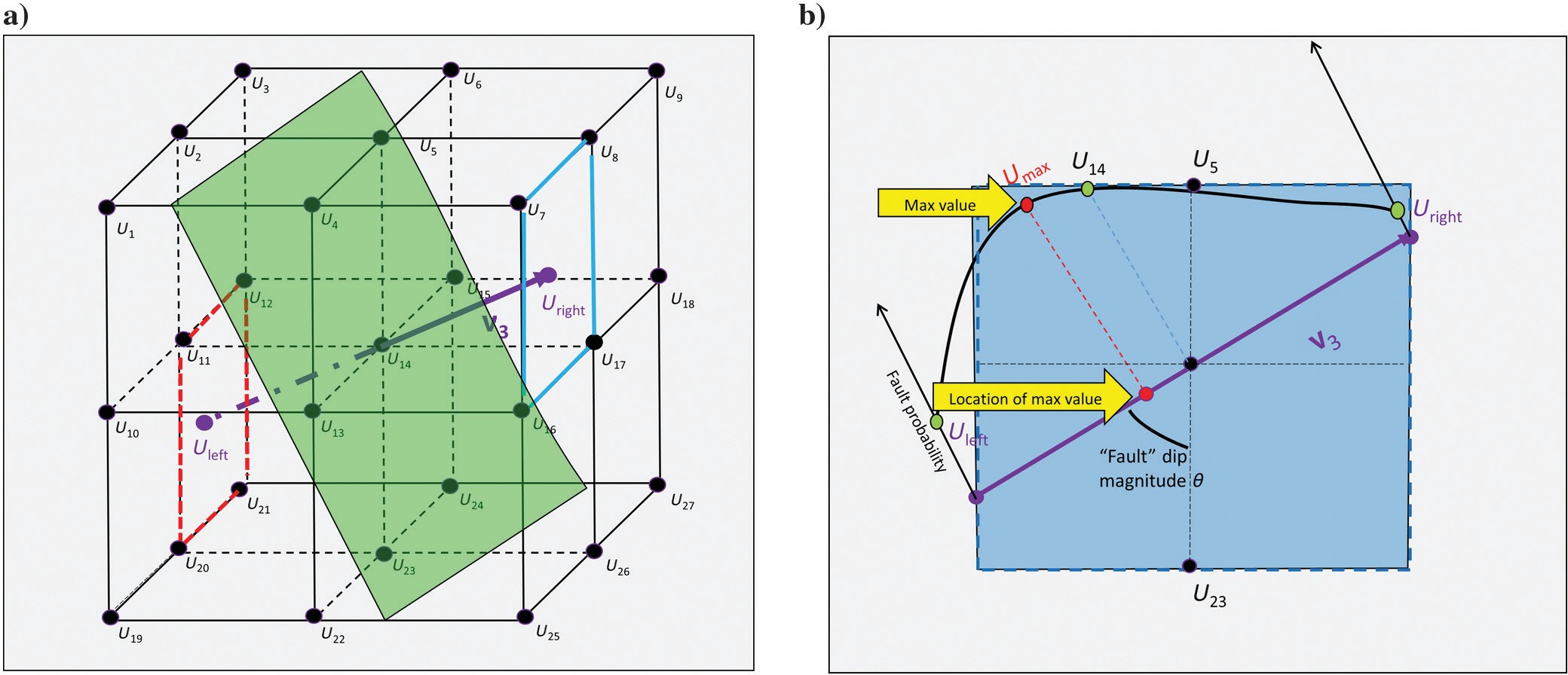
The intersection of v3 with this window gives the locations (Uleft, Uright), which fall in the 2D red and blue rectangles, and they are then interpolated from the neighboring grid points. We assume the center analysis point U14 is at (0, 0, 0) and the point U1 is at (−dx, −dy, −dz). Values of interpolated points Uleft and Uright in the analysis window (Figure 4) are
and
If the value at the center of the analysis window, U14 < Uleft or U14 < Uright, no fault maximum occurs and we set the skeletonized value to be zero. If the value at the center of the analysis window, U14 ≥ Uleft and U14 ≥ Uright, a fault anomaly falls within the window. We fit a parabola of the form
to the value Uleft, U14, and Uright (Figure 4b). The maximum value Umax and distance ξmax between U14 and location of Umax projection on the eigenvector v3 is
where a and b are defined as
where d is the half-length between U left and U right. In general, Umax does not fall on the grid point U14, such that we need to distribute the Umax value into the eight neighboring grid points and the weights functions wk are based on their distance between the Umax and eight neighboring grid points:
In Figure 5, Umax falls with a subcube of the grid-analysis window, indicated by the dashed red line. We compute skeletonized values on eight neighboring grid points whose weighted average produces the fault probability at the maximum location. Finally, all skeletonized values on the grid points will be output to the skeletonized image.
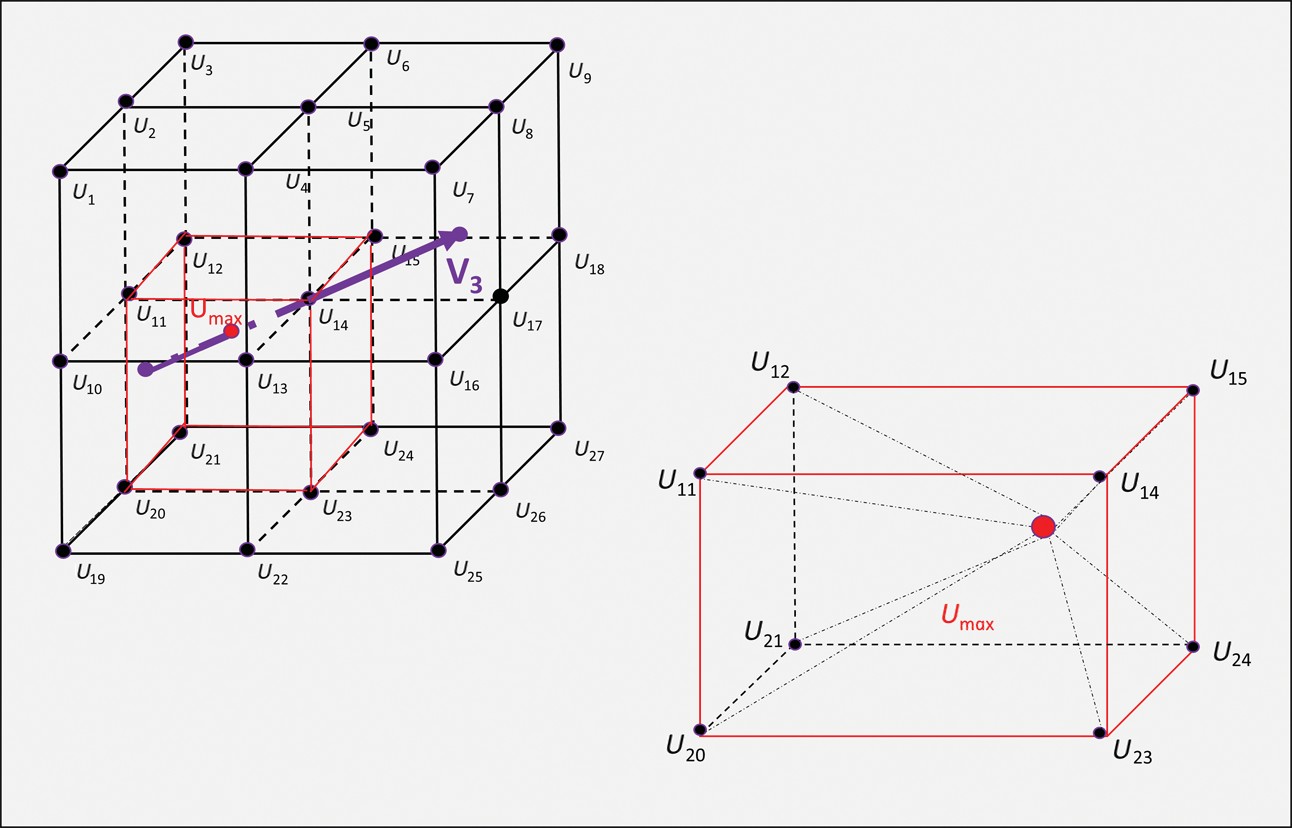
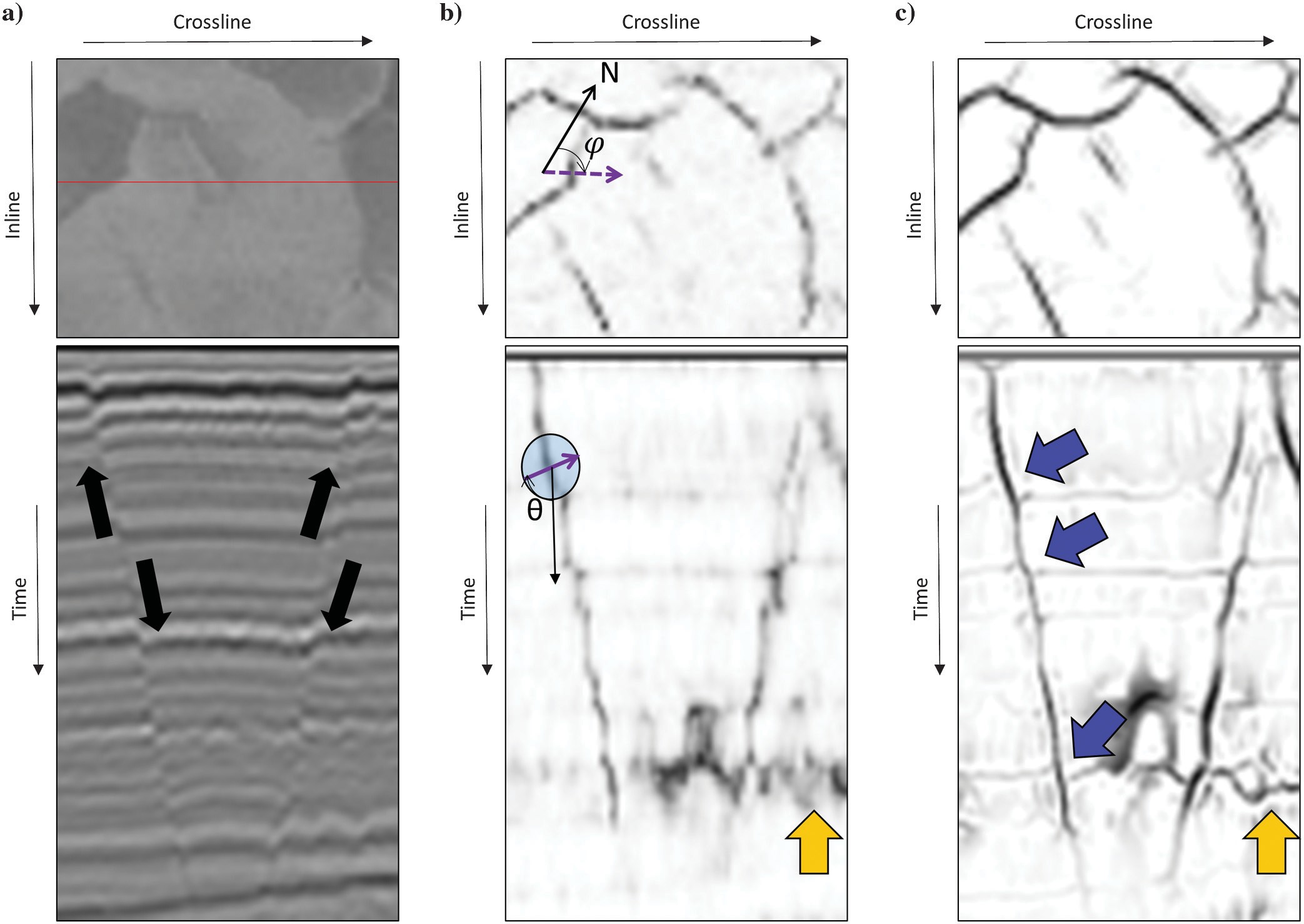
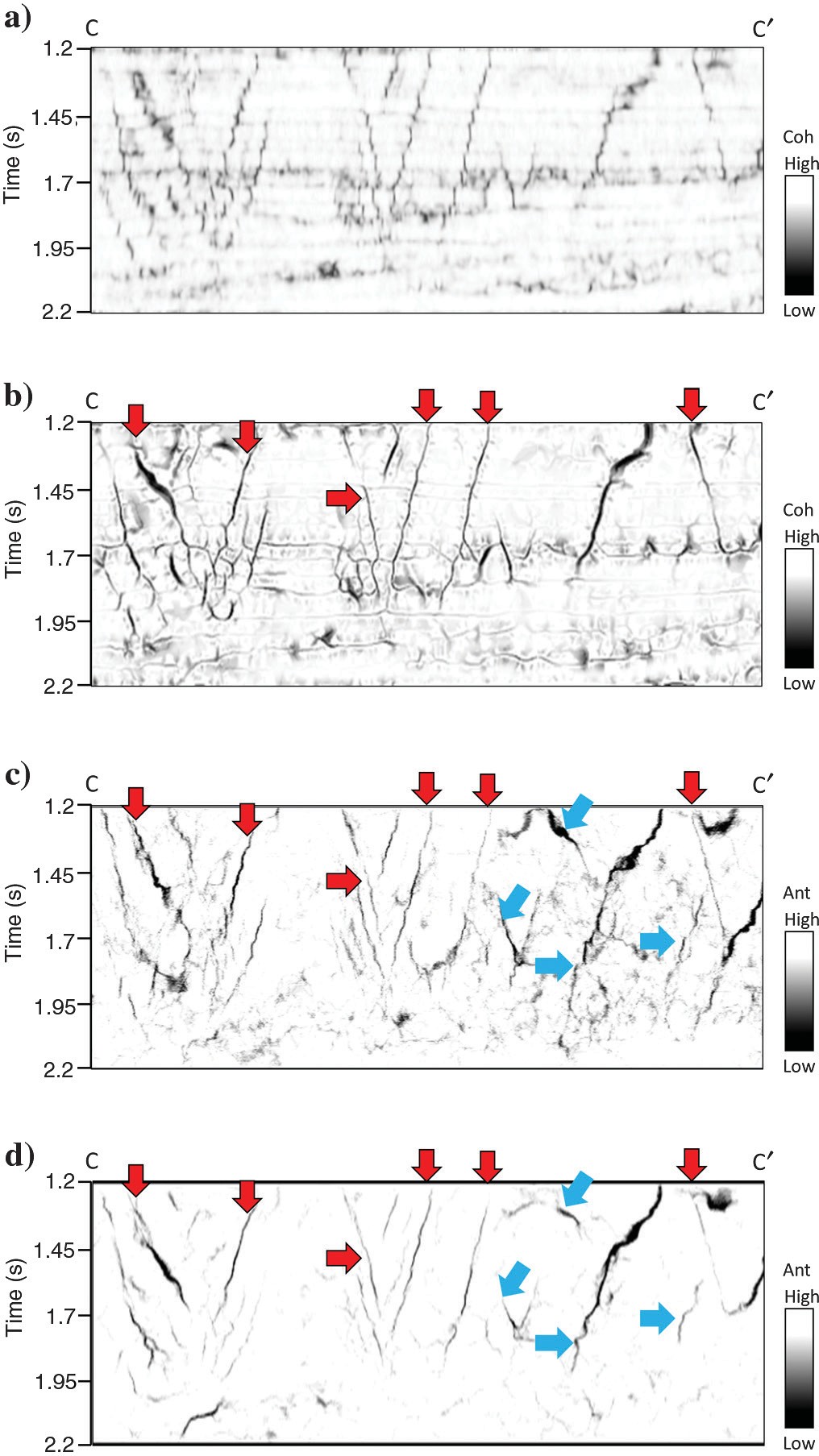
Figure 6 shows a normal fault before and after our directional skeletonization workflow. Coherence fault anomalies appear broken on the time slice (Figure 6b), whereas “stair-step” artifacts appear on the vertical slice. Fault-dip azimuth φ and fault-dip magnitude θ, which are computed from the eigenvector v3 indicate the direction of skeletonization, with the result shown in Figure 6. After this workflow, faults become sharper and more continuous. Stratigraphic features are also preserved, and these can be used to estimate fault throws that are indicated by the blue arrows in Figure 6c. Lateral discontinuities, such as shale-dewatering syneresis, are enhanced after our workflow that is indicated by yellow arrows.
Application
Gulf of Mexico (GOM3D)
We first apply our workflow to a 3D seismic data set in the Gulf of Mexico (GOM3D). The seismic data were acquired by Petroleum Geo-Services (PGS) using towed streamer acquisition with two sources and three receiver cables with a maximum offset of 6000 m. The data set within the inline and crossline spacing of 37.5 × 12.5 m (123.1 × 39.4 ft), covers more than 253 km2 (2723.27 ft2), and has been prestack time migrated. The uplift of the western salt dome is contemporaneous with the upper minibasin fill, and it occurred earlier than the eastern salt dome rise. Structural and stratigraphic features, such as salt domes, mass transport complexes (MTCs), and undeformed sediment and shale, are major seismic facies in this area. Figure 7 displays a time slice at 1 s and a vertical slice AA′ through the seismic amplitude volume. Random and coherent noise overprint reflectors in the migrated data set. After principal-component SOF (Figure 7c and 7d), the signal- to-noise ratio (S/N) of lateral and vertical discontinuities has increased, as seen in the clearer faults and block delineation within the MTCs. Figure 7e and 7f shows the rejected noise.

(f) vertical slice along line AA′ through the rejected “noise” volume. Note that the seismic amplitude volume after SOF shows a better S/N. All images are at the same scale amplitude.
Figure 8 shows the comparison of coherence before and after principal component SOF. Salt domes and MTCs exhibit a “salt-and-pepper” pattern in the coherence volume. Figure 8c and 8d shows that coherence computed after filtering preserves lateral and vertical discontinuities, and suppresses random and coherent noises. Coherence computed from the SOF seismic amplitude volume exhibits a better S/N. Small cross faults and other discontinuities within the MTCs are clearly imaged at the time (Figure 8c) and vertical slices (Figure 8d) through coherence. However, fault anomalies still exhibit the stair-step artifacts.
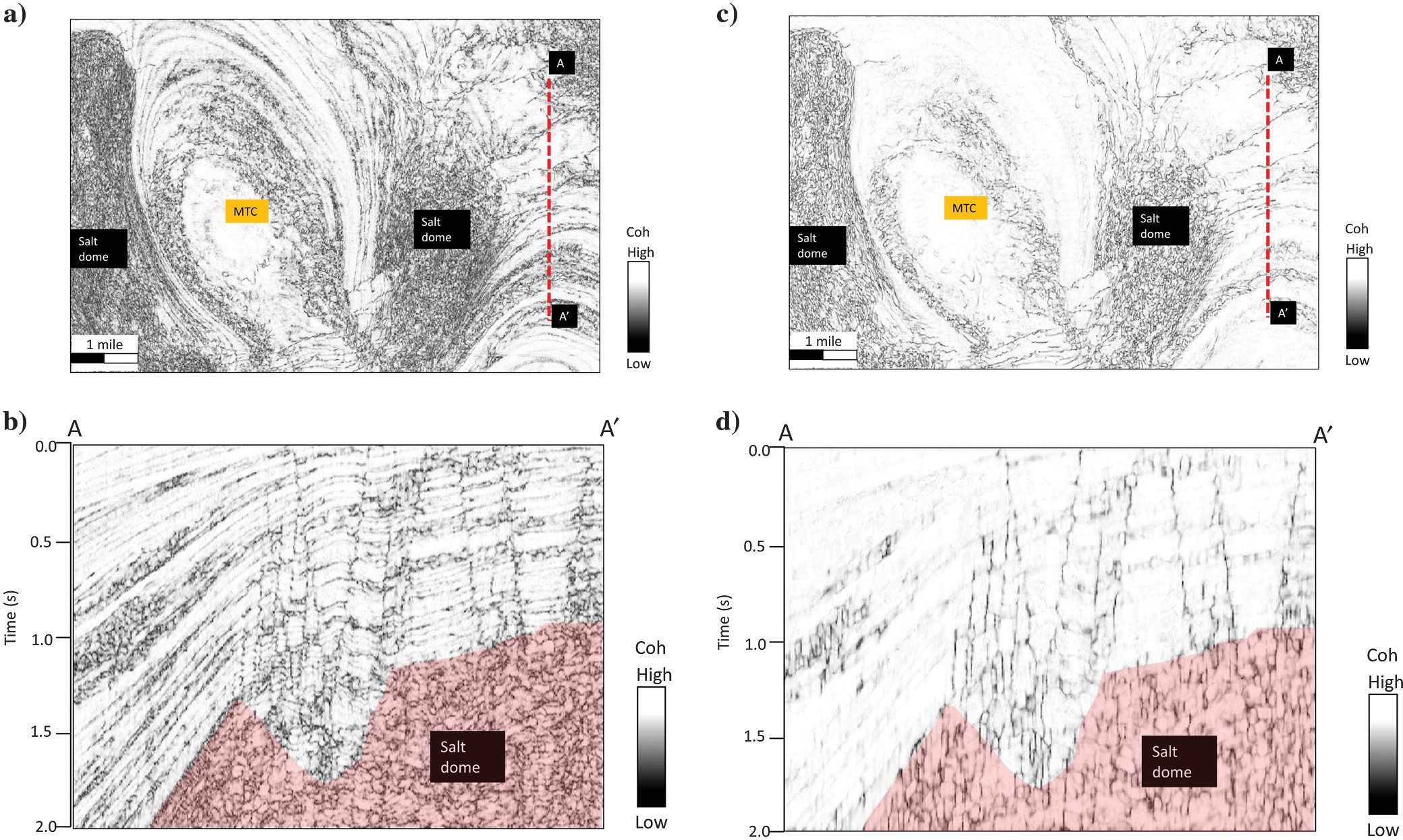
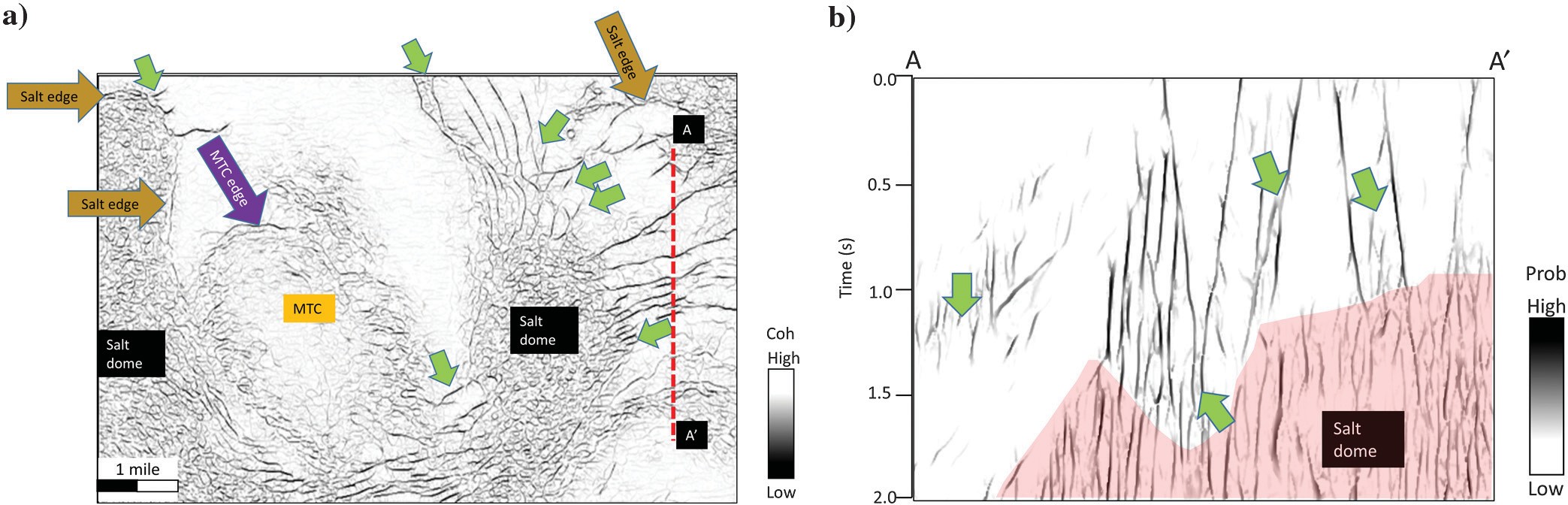
Figure 9a and 9b shows directionally skeletonized coherence images. Fault anomalies are now more continuous, exhibit higher contrast, with reduced stair-step artifacts. Salt edges, MTC edges, and many subtle faults (indicated by the green arrows in Figure 9) are enhanced in the time and vertical slices. The noise that does not represent locally planar discontinuities is suppressed during the skeletonization step.
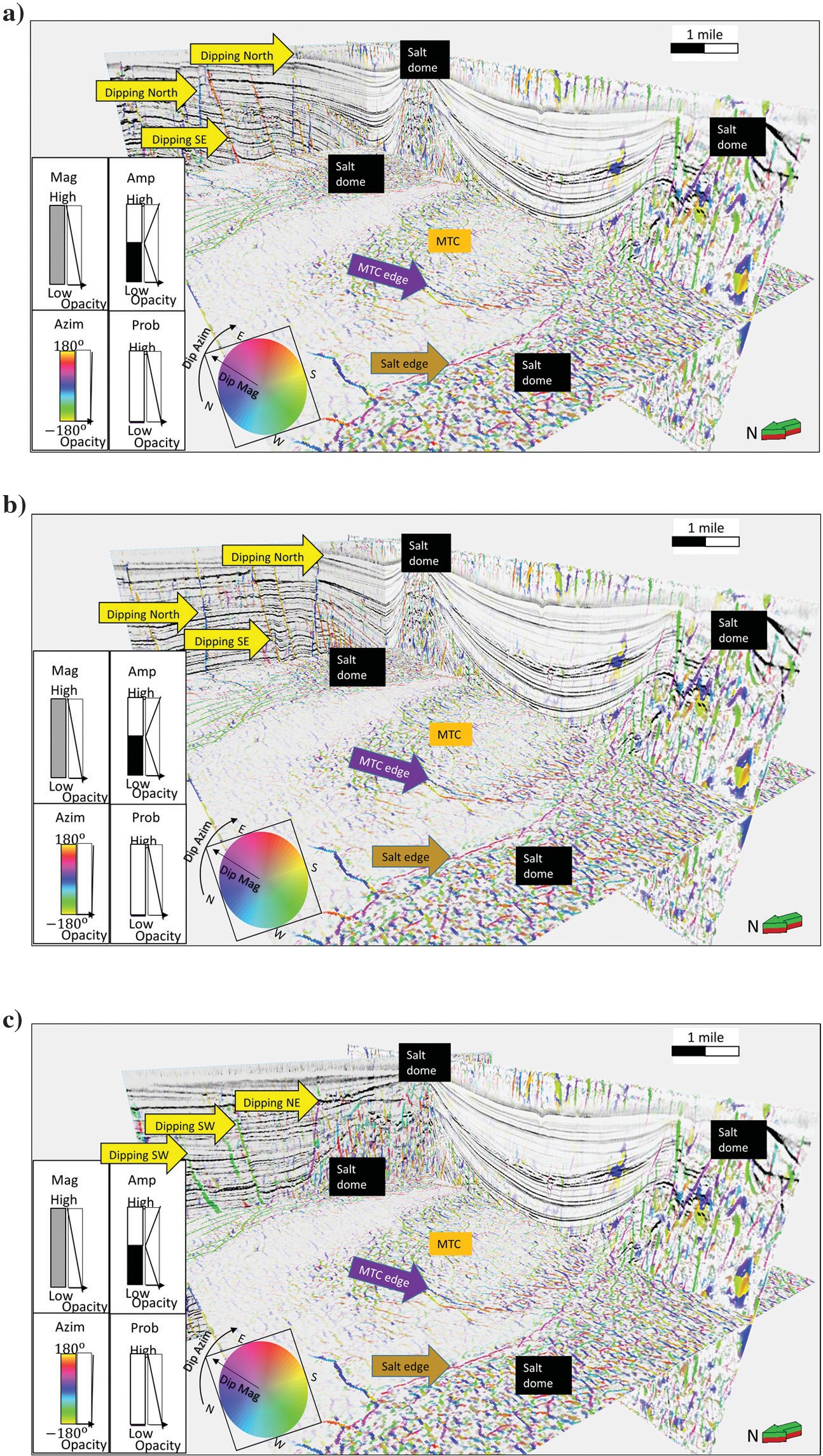
In Figure 10, we use the hue-lightness-saturation (HLS) color model to corender the fault-dip magnitude (against S), the skeletonized fault probability (against L), and the fault-dip azimuth (against H). In Figure 10, the fault orientation is readily seen. Numerical computation of fault probability and orientation at each voxel provide an easy way to identify fault sets, either visibly or through statistical analysis. Note that the coherent noise within the salt has been organized and should be interpreted as noise. More sophisticated processing produces homogeneous reflection salt images in this part of the Gulf of Mexico.
The S/N of this time-migrated data set was very low. We applied the workflow to this data set, and found significant improvement after applying our skeletonized fault probability workflow. However, there are still some spikes, which are poorly displayed. In terms of spikes, coherence values will always range between zero and one. For this reason, isolated spikes do not cause problems so long as they do not align with other spikes. The biggest limitation in applying attributes and skeletonization to this kind of data is that those interference phenomena corresponding to overlapping, poorly migrated events will give rise to discontinuities, which of course will then be sharpened. Such data limitations, including issues as basic as fault shadows, need to be properly addressed in the imaging algorithm, and they cannot be corrected by any data conditioning or image processing.
Gulf of Mexico (GOM3D)
Our second test data are from the Great South Basin, New Zealand. The intracontinental rift basin formed during the mid-Cretaceous and is divided into several highly faulted subbasins that contain very thick sedimentary fill. A polygonal fault system is very developed in the area, and its genetic mechanisms include gravity collapse, density inversion, syneresis, and compactional loading (Cartwright et al., 2003), whereas syneresis is also seen in the data set. The inline and crossline spaces are 12.5 m, and the time sample rate is 2 ms. Figure 11 shows the original seismic amplitude. We compute coherence from the seismic amplitude volume.

In Figure 12a, polygonal faults are well-delineated. However, the well-known stair-step artifacts are exhibited on the vertical slice (Figure 12c). The syneresis pattern (Figure 12b and 12c) is too chaotic to be interpreted. Fault trends in coherence are disconnected, especially on curved faults.
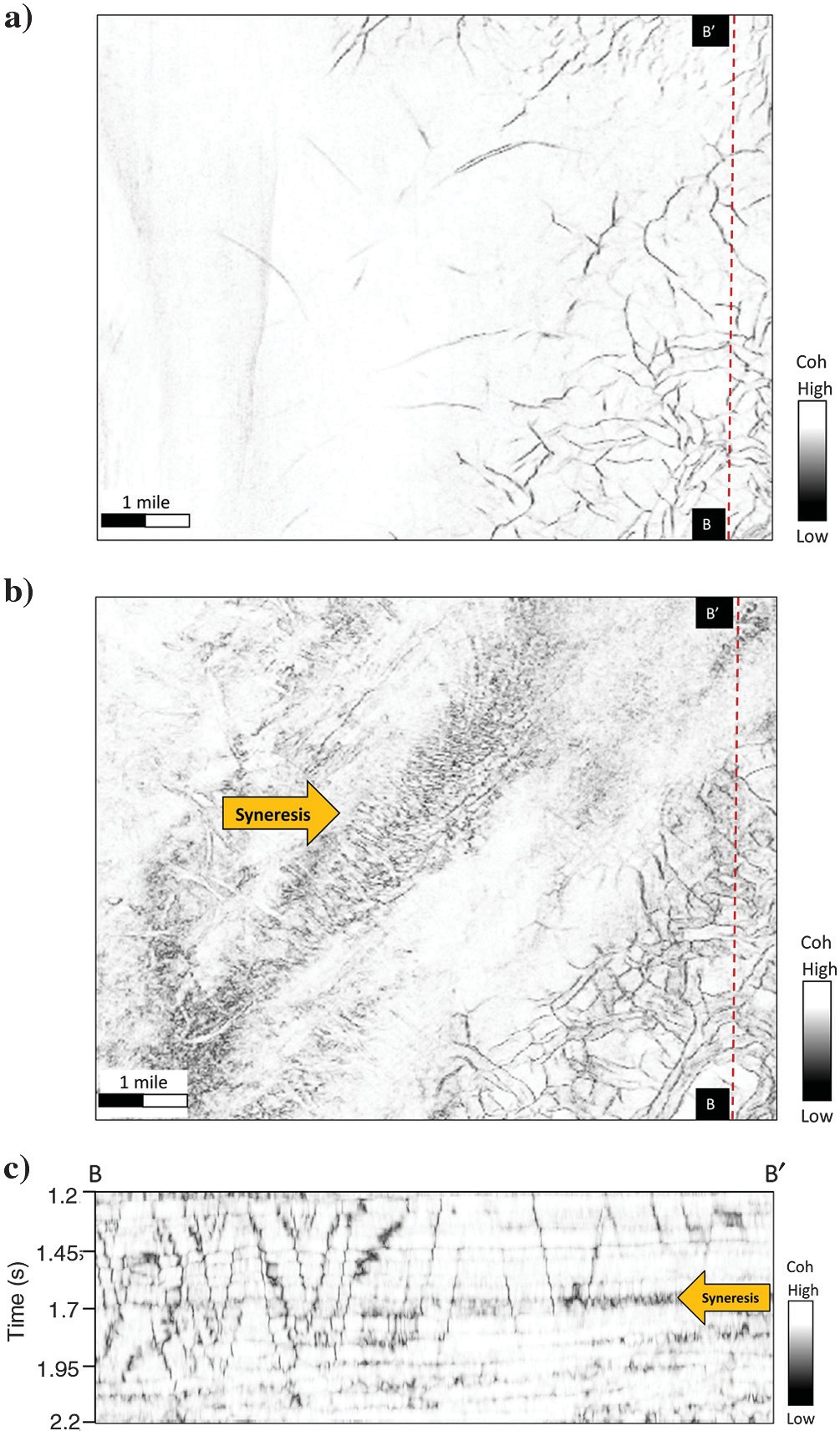
After our workflow (Figure 13), polygonal faults are sharper and more continuous, and stair-step artifacts have been suppressed. Syneresis and other stratigraphic features are also enhanced after skeletonization. The “thick” black smears correspond to faults subparallel to the vertical slices.
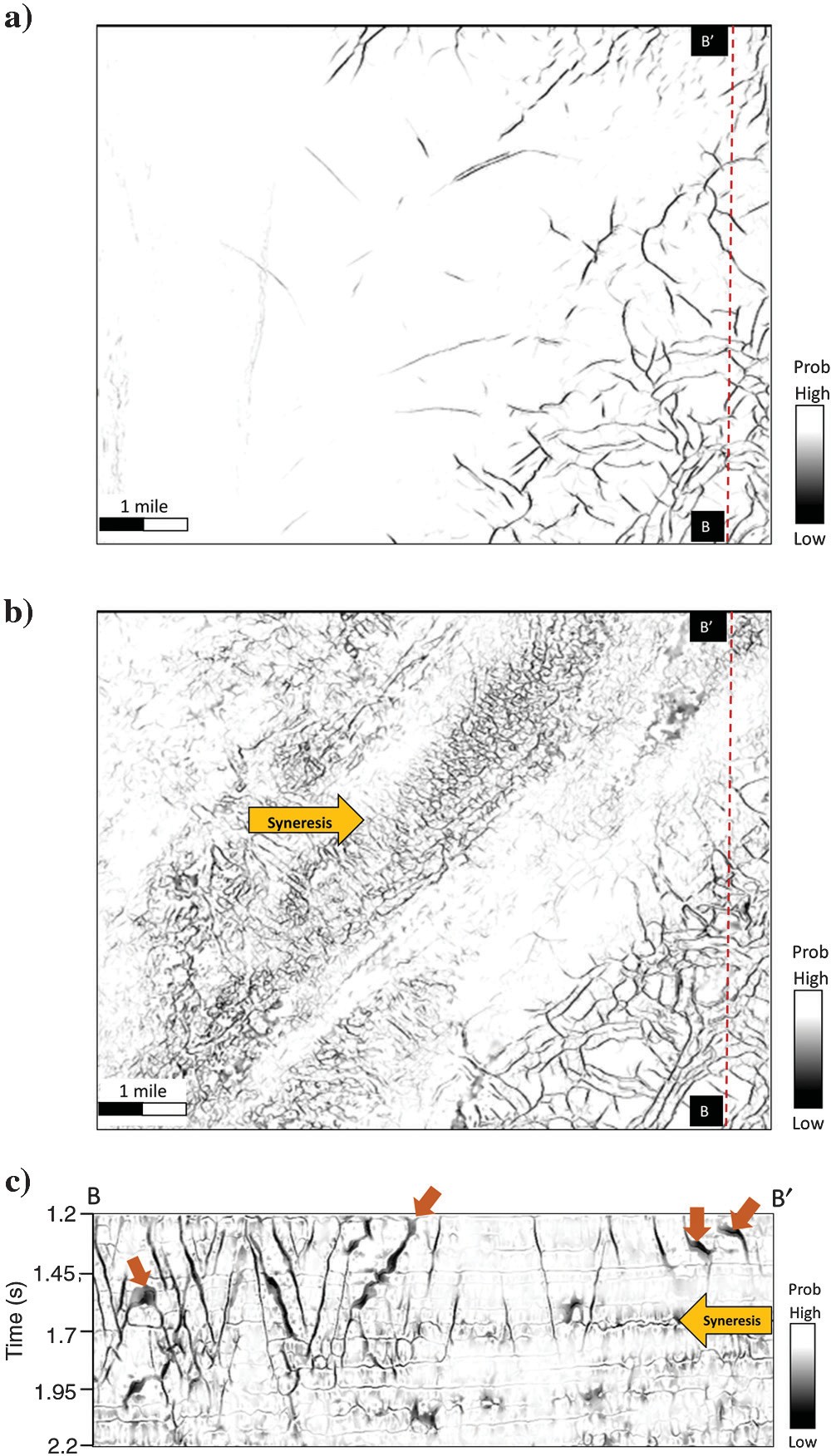
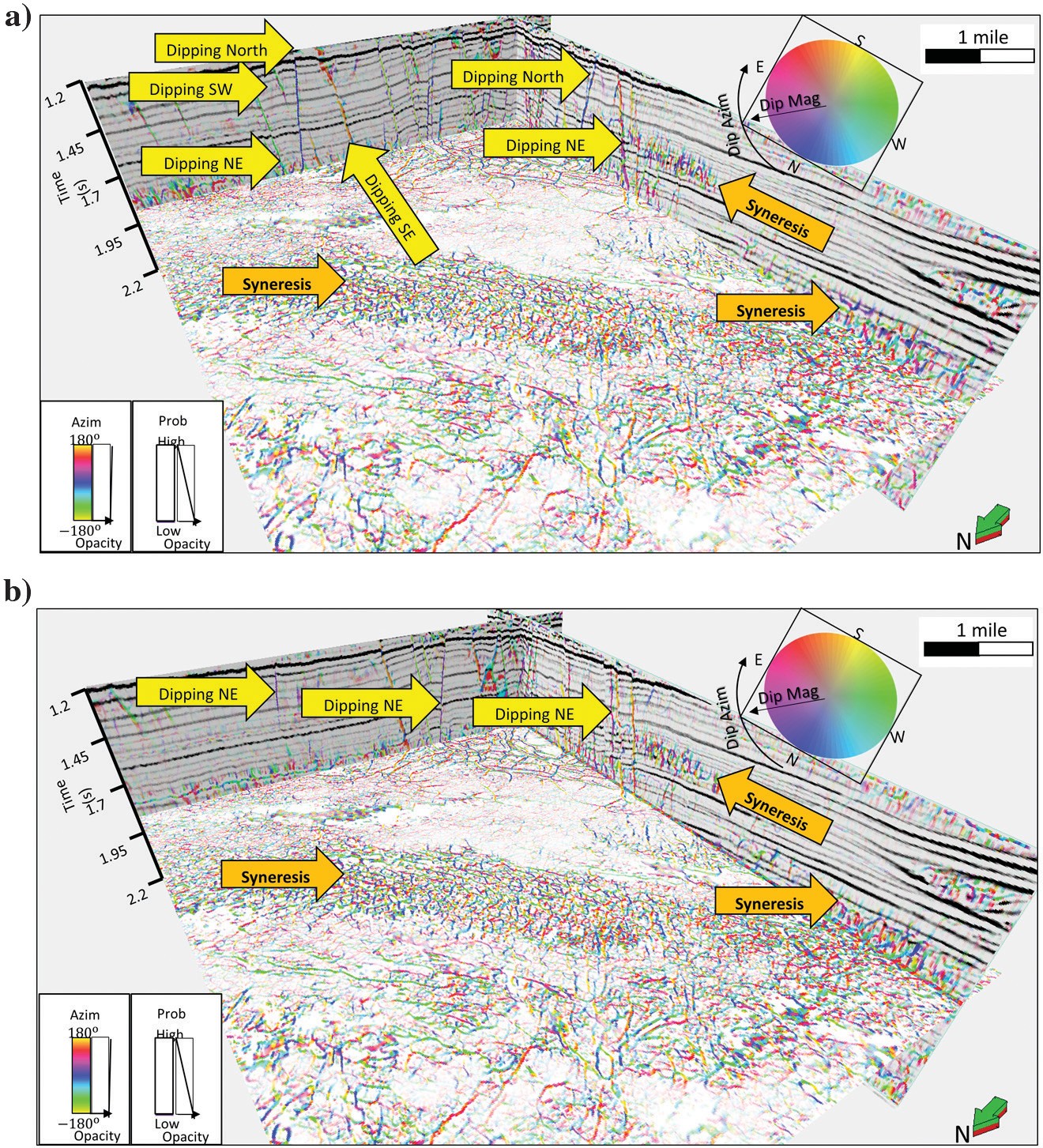
Figure 14 shows a 3D view of a skeletonized fault probability corendered with fault dip azimuth and seismic amplitude data. Note that polygonal fault planes and syneresis are preserved after directional skeletonization in the 3D volume, and fault planes associated with fault dip azimuth are readily identified. Lateral discontinuities, such as syneresis, are also seen.
Comparison of directional skeletonization with swarm intelligence
We apply our directional skeletonization method and swarm intelligence to the GSB3D survey, and we compare these results in fault and syneresis enhancement. Figure 15a shows a time slice at 1.72 s through the coherence volume that is used as the input for comparison of the two different methods. Polygonal faults (green rectangular) and syneresis (orange arrow) are present in this time slice. Figure 15b shows the directional skeletonization result, and Figure 15c shows the result of swarm intelligence, both computed from coherence. Note that, directional skeletonization shows more details (subtle faults) than does swarm intelligence in the polygonal fault zone. Swarm intelligence generates linear artifacts, but directional skeletonization does not, as indicated by the red arrows in Figure 15c and 15d. Figure 15d shows the swarm intelligence result with the directionally skeletonized volume as input. The results obtained by applying swarm intelligence to the directionally skeletonized data are better than those obtained from coherence, preserving more subtle discontinuities in the polygonal faults zone. However, despite applying many different combinations of parameters for swarm intelligence, the syneresis area could not be preserved (orange arrow). We conclude with Figure 16 showing the same volumes as in Figure 15 but on vertical slices.
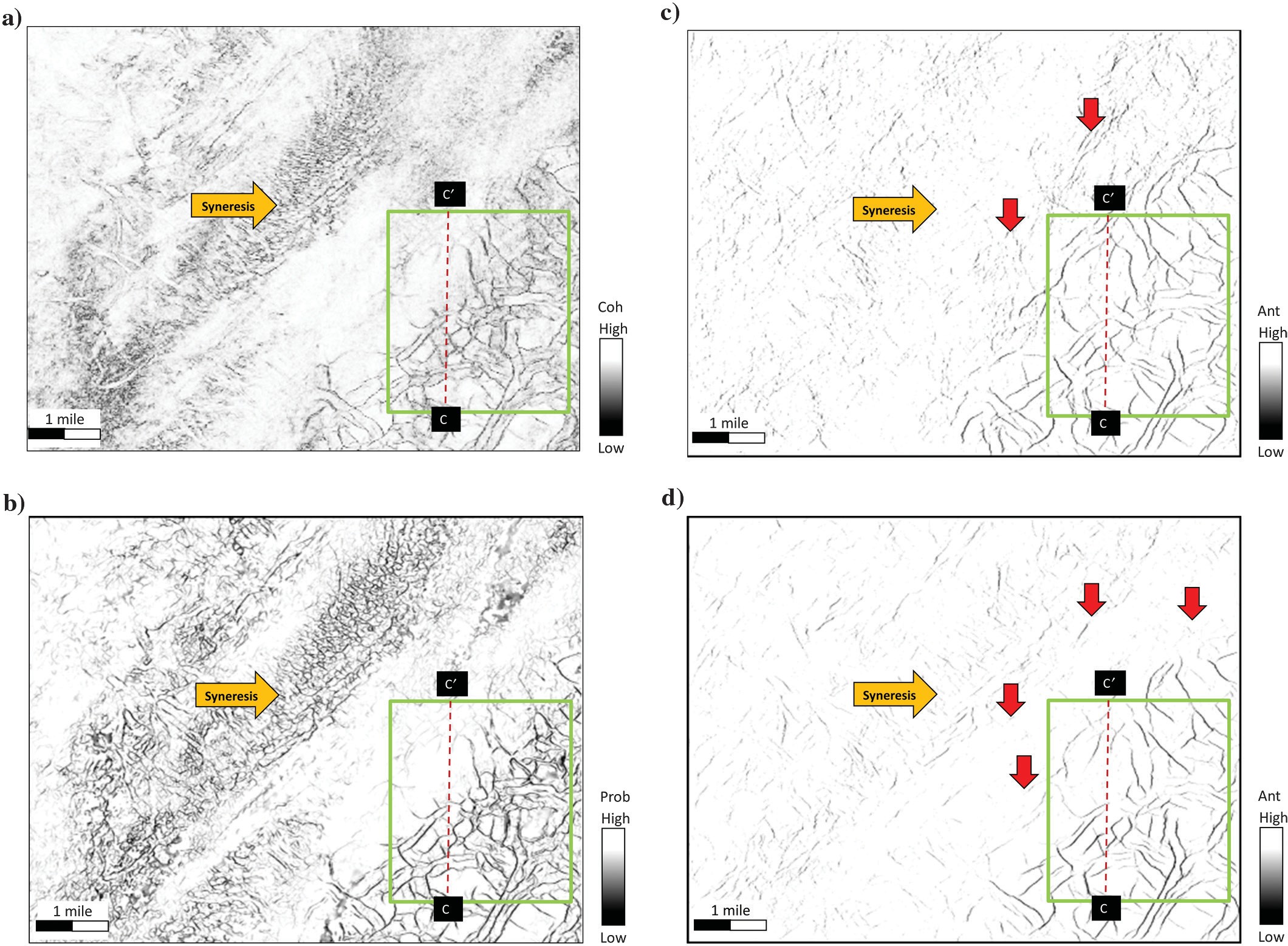
The swarm intelligence result with directional skeletonization volume as input shows more continuous and sharper fault images than the one computed directly from coherence. The directional skeletonization workflow in Figure 16 exhibits fewer stair-step artifacts than those in Figure 16 (red arrows). The blue arrows indicate faults better mapped by swarm intelligence than by directional skeletonization, at the expense of organizing other features that are probably noise. Stratigraphic features are preserved and enhanced using the directional skeletonization workflow. Comparing Figure 16c with Figure 16d, we can see that swarm intelligence with directional skeletonization as input created fewer artifacts. Swarm intelligence and the skeletonization workflow need the edge-detection attribute as input. These two methods are sample-by-sample analysis, and the computation cost of these two methods is similar. For the data set GSB3D with 500 × 280 traces and 750 time samples, the enhancement and skeletonization take approximately 200 s. Applying the same data set to swarm intelligence, the computation time is approximately 220 s.
Conclusions
We have developed a 3D fault-directional skeletonization workflow to skeletonize and segment fault images. First, we applied SOF to suppress random and coherent noise. Next, we computed coherence as our edge-detection attribute to detect discontinuous features. Coherence computed after data conditioning using SOF, followed by iterative application of a LoG filter and directional skeletonization rejects noise, enhances faults in the vertical and lateral directions. We skeletonize the results perpendicular to the fault-dip azimuth and dip magnitude, resulting in a sharper, more continuous fault and stratigraphic edges. These discontinuous features can be color coded by their dip azimuth and magnitude or as a suite of independent, azimuthally limited fault sets that may be found to have greater risk of communicating with adjacent aquifers, or on the positive side, to be better correlated with open fractures. Subtle, stratigraphically limited features such as faults within MTCs and syneresis in shales are also enhanced. Multiattribute displays of the skeletonized faults and its dip magnitude and azimuth readily show the interfault relationships. Comparing our directional skeletonization workflow with swarm intelligence, we find that swarm intelligence has the danger of enhancing small artifacts, which are not present in our skeletonization results. Swarm intelligence and directional skeletonization reduce stair-step artifacts, and connect previously discontinuous fault segments. Our skeletonization workflow preserves stratigraphic features, such as dewatering syneresis, which swarm intelligence smears. Cascading directional skeletonization with swarm intelligence results in more continuous and sharper fault imaging than with coherence as the input.
Acknowledgments
We thank the sponsors of the OU Attribute-Assisted Processing and Interpretation Consortium for their guidance and their financial support.
References
AlBinHassan, N. M., and K. J. Marfurt, 2003, Fault detection using Hough transforms: 73rd Annual International Meeting, SEG, Expanded Ab- stracts, 1719–1721.
Bakker, P., L. J. van Vliet, and P. W. Verbeek, 1999, Edge-preserving ori- entation adaptive filtering: Proceedings IEEE-CS Conference on Com- puter Vision and Pattern Recognition, 535–540.
Barnes, A. E., 2006, A filter to improve seismic discontinuity data for fault interpretation: Geophysics, 71, no. 3, P1–P4, doi: 10.1190/1.2195988.
Boe, T. H., 2012, Enhancement of large faults with a windowed 3D Radon transform filter: 82nd Annual International Meeting, SEG, Expanded Ab- stracts, doi: 10.1190/segam2012-1008.1.
Cartwright, J. A., D. James, and A. Bolton, 2003, The genesis of polygonal fault systems: A review, in P. Van Rensbergen, R. R. Hillis, A. J. Maltman, and C. K. Morley, eds., Subsurface sediment mobilization: Geological Society of London, Special Publications, 223–242.
Cohen, I., N. Coult, and A. A. Vassiliou, 2006, Detection and extraction of fault surfaces in 3D seismic data: Geophysics, 71, no. 4, P21–P27, doi: 10.1190/1.2215357.
Davogustto, O., and K. J. Marfurt, 2011, Removing acquisition footprint from legacy data volumes: 81st Annual International Meeting, SEG, Ex- panded Abstracts, 1025–1029.
Dewett, D. T., and A. A. Henza, 2016, Spectral similarity fault enhancement: Interpretation, 4, no. 1, SB149–SB159, doi: 10.1190/INT-2015-0114.1.
Dorn, G. A., B. Kadlec, and P. Murtha, 2012, Imaging faults in 3D seismic volumes: 82nd Annual International Meeting, SEG, Expanded Abstracts, doi: 10.1190/segam2012-1538.1.
Fehmers, G., and C. F. W. Höcher, 2003, Fast structural interpretation with structure-oriented filtering: Geophysics, 68, 1286–1293, doi: 10.1190/1.1598121.
Gersztenkorn, A., and K. J. Marfurt, 1999, Eigenstructure based coherence computations as an aid to 3D structural and stratigraphic mapping: Geo- physics, 64, 1468–1479, doi: 10.1190/1.1444651.
Hale, D., 2013, Methods to compute fault images, extract fault surfaces, and estimate fault throws from 3D seismic images: Geophysics, 78, no. 2, O33–O43, doi: 10.1190/geo2012-0331.1.
Henderson, J., S. J. Purves, and G. Fisher, 2008, Delineation of geological elements from RGB color blending of seismic attributes using a sem- blance-based coherency algorithm: The Leading Edge, 27, 342–350, doi: 10.1190/1.2896625.
Kadlec, B., G. Dorn, H. Tufo, and D. Yuen, 2008, Interactive 3-D compu- tation of fault surfaces using level sets: Visual Geoscience, 13, 133–138, doi: 10.1007/s10069-008-0016-9.
Li, F., and W. Lu, 2014, Coherence attribute at different spectral scales: In- terpretation, 2, no. 1, SA99–SA106, doi: 10.1190/INT-2013-0089.1.
Luo, Y., 2002, Edge-preserving smoothing and applications: The Leading Edge, 21, 136–158, doi: 10.1190/1.1452603.
Luo, Y., W. G. Higgs, and W. S. Kowalik, 1996, Edge detection and strati- graphic analysis using 3D seismic data: 66th Annual International Meet- ing, SEG, Expanded Abstracts, 324–327.
Machado, G., A. Alali, B. Hutchinson, O. Olorunsola, and K. J. Marfurt, 2016, Display and enhancement of volumetric fault image: Interpretation, 4, no. 1, SB51–SB61, doi: 10.1190/INT-2015-0104.1.
Marfurt, K. J., 2006, Robust estimates of 3D reflector dip and azimuth: Geo- physics, 71, no. 4, P29–P40, doi: 10.1190/1.2213049.
Marfurt, K. J., 2015, Techniques and best practices in multiattribute display: Interpretation, 3, no. 1, B1–B23, doi: 10.1190/INT-2014-0133.1.
Marfurt, K. J., R. L. Kirlin, S. H. Farmer, and M. S. Bahorich, 1998, 3D seismic attributes using a running window semblance-based algorithm: Geophysics, 63, 1150–1165, doi: 10.1190/1.1444415.
Pedersen, S., T. Randen, L. Sonneland, and O. Steen, 2002, Automatic 3D fault interpretation by artificial ants: 72nd Annual International Meeting, SEG, Expanded Abstracts, 512–515.
Qi, J., F. Li, B. Lyu, O. Olorunsola, K. J. Marfurt, and B. Zhang, 2016, Seismic fault enhancement and skeletonization: 86th Annual International Meeting, SEG, Expanded Abstracts, 1966–1970.
Qi, J., T. Lin, T. Zhao, F. Li, and K. J. Marfurt, 2016, Semisupervised multi- attribute seismic facies analysis: Interpretation, 4, no. 1, SB91–SB106, doi: 10.1190/INT-2015-0098.1.
Qi, J., B. Zhang, H. Zhou, and K. J. Marfurt, 2014, Attribute expression of fault-controlled karst — Fort Worth Basin, TX: Interpretation, 2, no. 3, SF91–SF110, doi: 10.1190/INT-2013-0188.1.
Randen, T., S. Pedersen, and L. Sønneland, 2001, Automatic extraction of fault surfaces from three-dimensional seismic data: 71st Annual International Meeting, SEG, Expanded Abstracts, 551–554.
Wallet, B., V. Aarre, A. Davids, T. Dao, and K. J. Marfurt, 2011, Using a hue-saturation color map to visualize dewatering faults in the overburden of the Hod Field, North Sea: 81st Annual International Meeting, SEG, Expanded Abstracts, 946–950.
Wang, X., J. Gao, C. Chen, C. Yang, and Z. Zhu, 2016, Detecting method of seismic discontinuities based on high dimensional continuous wavelet transform (in Chinese): Chinese Journal of Geophysics, 29, 3394–3407.
Wu, X., and D. Hale, 2015, 3D seismic image processing for faults: Geo-physics, 81, no. 2, IM1–IM11, doi: 10.1190/geo2015-0380.1.
Wu, X., and D. Hale, 2016, Automatically interpreting all faults, unconformities, and horizons from 3D seismic images: Interpretation, 4, no. 2, T227– T237, doi: 10.1190/INT-2015-0160.1.
Zhang, B., D. Chang, T. Lin, and K. J. Marfurt, 2015, Improving the quality of prestack inversion by prestack data conditioning: Interpretation, 3, no. 1, T5–T12, doi: 10.1190/INT-2014-0124.1.
Zhang, B., Y. Liu, M. Pelissier, and N. Hemstra, 2014, Semiautomated fault interpretation based on seismic attributes: Interpretation, 2, no. 1, SA11– SA19, doi: 10.1190/INT-2013-0060.1.