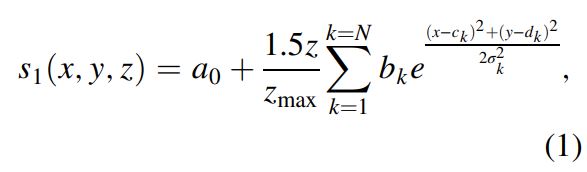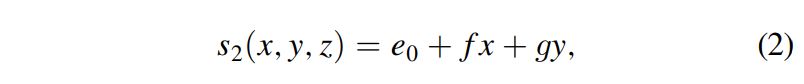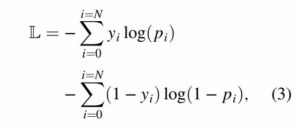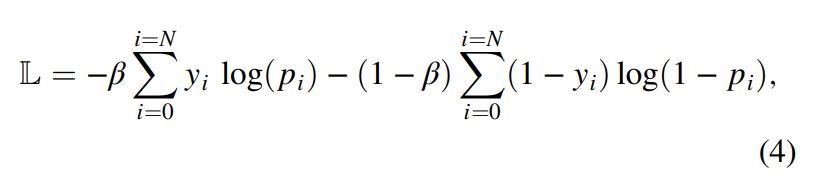Using Synthetic Data Sets to Train an End-to-End Convolutional Neural Network for 3D Seismic Fault Segmentation

Abstract

Delineating faults from seismic images is a key step for seismic structural interpretation, reservoir characterization, and well placement. In conventional methods, faults are considered as seismic reflection discontinuities and are detected by calculating attributes that estimate reflection continuities or discontinuities. We consider fault detection as a binary image segmentation problem of labeling a 3D seismic image with ones on faults and zeros elsewhere. We have performed an efficient image-to-image fault segmentation using a supervised fully convolutional neural network. To train the network, we automatically create 200 3D synthetic seismic images and corresponding binary fault labeling images, which are shown to be sufficient to train a good fault segmentation network. Because a binary fault image is highly imbalanced between zeros (nonfault) and ones (fault), we use a class-balanced binary cross-entropy loss function to adjust the imbalance so that the network is not trained or converged to predict only zeros. After training with only the synthetic data sets, the network automatically learns to calculate rich and proper features that are important for fault detection. Multiple field examples indicate that the neural network (trained by only synthetic data sets) can predict faults
from 3D seismic images much more accurately and efficiently than conventional methods. With a TITAN Xp GPU, the training processing takes approximately 2 h and predicting faults in a 128 × 128 × 128 seismic volume takes only milliseconds.

Introduction

Faults are typically recognized as lateral reflection discontinuities in a 3D seismic image. Based on this observation, numerous methods have been proposed to detect faults by calculating attributes of measuring seismic reflection continuity such as semblance (Marfurt et al., 1998) and coherency (Marfurt et al., 1999; Li and Lu, 2014; Wu, 2017), or reflection discontinuity such as variance (Van Bemmel and Pepper, 2000; Randen et al., 2001) and gradient magnitude (Aqrawi and Boe, 2011). These seismic attributes, however, can be sensitive to noise and stratigraphic features, which also correspond to reflection discontinuities in a seismic image. This means that measuring seismic reflection continuity or discontinuity alone is insufficient to detect faults (Hale, 2013).

Faults are typically more vertically aligned, whereas stratigraphic features mostly extend laterally. Based on this observation, Gersztenkorn and Marfurt (1999) suggest using vertically elongated windows in computing seismic coherence to enhance faults while suppressing the stratigraphic features. Similarly, some other authors (Bakker, 2002; Hale, 2009; Wu, 2017) apply smoothing in directions perpendicular to seismic reflections in computing coherence or semblance by assuming that faults are typically normal to reflections. However, faults are seldom vertical or are not necessarily perpendicular to seismic reflections. Therefore, some authors (Hale, 2013; Wu and Hale, 2016) propose smoothing the numerator and denominator of the semblance along fault strikes and dips to compute the fault-oriented semblance or fault likelihood. However, calculating fault-oriented semblance is computationally more expensive than the previous attributes because it requires scanning over all possible combinations of fault strikes and dips to find the maximum fault likelihoods.

Some fault detection methods start with some initial fault attributes and further enhance them by smoothing the attributes along fault strikes and dips (Neff et al., 2000; Cohen et al., 2006; Wu and Zhu, 2017). These methods also need to smooth the fault attributes over all possible combinations of fault strikes and dips to obtain the best enhanced fault features. Similarly, some authors (Pedersen et al., 2002, 2003) propose to enhance fault features along paths of “artificial ants” by assuming that the paths follow faults. Wu and Fomel (2018) propose an efficient method to extract optimal surfaces following maximum fault attributes and use these optimal surfaces to vote for enhanced fault images of fault probabilities, strikes, and dips.

Recently, some convolutional-neural-network (CNN) methods have been introduced to detect faults by pixel-wise fault classification (fault or nonfault) with multiple seismic attributes (Huang et al., 2017; Di et al., 2018; Guitton, 2018; Guo et al., 2018; Zhao and Mukhopadhyay, 2018). Wu et al. (2018) use a CNN-based pixel-wise classification method to not only predict the fault probability but also estimate the fault orientations at the same time. These methods need to choose a local window or cube to make fault prediction at every image pixel, which is computationally highly expensive, especially in 3D fault detection. In this paper, we consider the fault detection as a more efficient end-to-end binary image segmentation problem by using CNNs. Image segmentation has been well-studied in computer science, and multiple powerful CNN architectures (e.g., Girshick et al., 2014; Ren et al., 2015; Ronneberger et al., 2015; Xie and Tu, 2015; Badrinarayanan et al., 2017; He et al., 2017) have been proposed to obtain superior segmentation results.

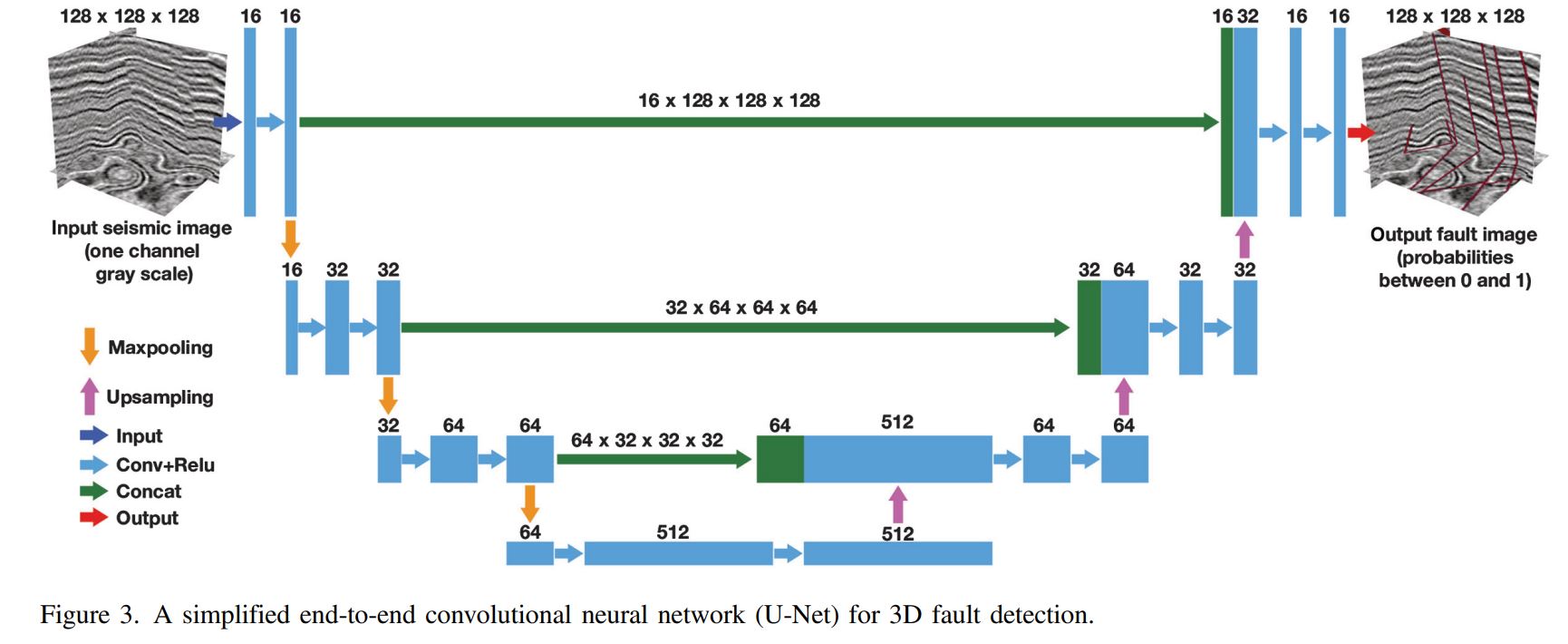
In this paper, we use an efficient end-to-end CNN, simplified from U-Net (Ronneberger et al., 2015), to perform our task of 3D binary fault segmentation. We simplify the original U-Net by reducing the number of convolutional layers and features at each layer, which significantly saves graphics processing unit (GPU) memory and computational time but still preserves high performance in our 3D fault detection tasks. Considering a fault binary image is highly biased with mostly zeros but only very limited ones on the faults, we use a balanced cross-entropy loss function for optimizing the parameters of our CNN model. To train and validate the neural network, we design a workflow to automatically generate 3D synthetic seismic and corresponding fault images. In this workflow, the seismic folding and faulting structures, wavelet peak frequencies, and noise are defined by a set of parameters, and each parameter can be chosen from some predefined range. By randomly choosing a combination of these parameters within the predefined ranges, we are able to generate numerous unique seismic images and corresponding fault labeling images. We train and validate, respectively, by using 200 and 20 pairs of synthetic seismic and fault images, which turned to be sufficient to train a good CNN model for our fault detection tasks. Although trained by using only synthetic seismic data sets, our CNN model can work much better and more efficiently than the conventional methods for 3D fault detection in field seismic data sets that are recorded at totally different surveys. By using a TITAN Xp GUP, our CNN model takes less than 5 min to predict faults in a large seismic volume with 450 × 1950 × 1200 samples.

Trainging Data Sets

Training and validating a CNN model often requires a large amount of images and corresponding labels. Manually labeling or interpreting faults in a 3D seismic image could be extremely time consuming and highly subjective. In addition, inaccurate manual interpretation, including mislabeled and unlabeled faults, may mislead the learning process. To avoid these problems, we propose an effective and efficient way to create synthetic seismic images and corresponding fault labels for training and validating our CNN model.

Synthetic seismic and fault images

Figure 1. The workflow of creating 3D synthetic training data sets. We first generate a horizontal reflectivity model (a) with a sequence of random numbers between −1 and 1. We then add some folding structures (b) to the model by vertically shearing the model and the shearing shifts are defined by a combination of several 2D Gaussian functions. We also add some planar shearing (c) to the model to increase the complexity of folding structures. We further add planar faulting to the model to obtain a folded and faulted reflectivity model (d). We finally convolve the reflectivity model with a Ricker wavelet to obtain a synthetic seismic image (e) and add some random noise to obtain a final image (f).

The workflow that we use to create synthetic seismic and fault images is similar to the one used for generating synthetic data sets by Wu and Hale (2016). In this workflow, we first generate a 1D horizontal reflectivity model r(x; y; z) (Figure 1a) with a sequence of random values that are in the range of [−1; 1]. We then create some folding structures in the reflectivity model by vertically shearing the model. We define the folding structures by using the following function:

which combines with multiple 2D Gaussian functions and a linear-scale function 1.5z/zmax. The combination of 2D Gaussian functions yields laterally varying folding structures, whereas the linear-scale function damps the folding vertically from below to above. In this equation, each combination of the parameters a0; bk; ck; dk, and σk yields some specific spatially varying folding structures in the model. By randomly choosing each of the parameters from the predefined ranges, we are able to create numerous models with unique structures. With the shift map s1 (x; y; z), we use a sinc interpolation to vertically shift the original reflectivity model r(x; y; z) to obtain a folded model r(x; y; z + s1(x; y; z)) as shown in Figure 1b. To further increase the complexity of the structures in the model, we also add some planar shearing defined as follows:

where the shearing shifts are laterally planar while being vertically invariant. The parameters e0; f, and g, again, are randomly chosen from some predefined ranges. By sequentially applying the planar shifts s2(x; y; z) to the previously folded model r(x; y; z + s1(x; y; z)), we obtain a new reflectivity model r(x; y; z + s1 + s2) as shown in Figure 1c.

After obtaining a folded reflectivity model, we then add planar faulting in the model. Although all the faults are planar, the fault orientations (dip and strike) and displacements of the faults are all different from each other. The fault displacements on each fault are allowed to be spatially varying along the directions of fault strike and dip. The common patterns of fault displacement distribution have been discussed by some authors (Muraoka and Kamata, 1983; Mansfield and Cartwright, 1996; Stewart, 2001). In generating faults in our synthetic models, we define the fault displacement distributions as a Gaussian function or linear function. In the case of Gaussian distribution, the fault displacements decrease from the fault center in all directions along the fault plane. In the other case of linear distribution, the fault displacements linearly increase (normal fault) or decrease (reverse fault) in the fault dip direction along the fault plane. The maximum fault displacement for each fault is randomly chosen in the range between 0 and 40 samples. From our experience, the images with more faults are more effective than those with fewer faults to train a CNN for fault segmentation. We therefore add more than five faults within a training image with the size of 128 × 128 × 128. However, these faults should not be too close to each other as shown in Figure 1d, in which we have added six planar faults.

After creating a folded and faulted reflectivity model (Figure 1d), we finally convolve this model with a Ricker wavelet to obtain a 3D seismic image shown in Figure 1e. The peak frequency of the wavelet is also randomly chosen from a predefined range. Note that we convolve the reflectivity model with a wavelet after (not before) creating the folding and faulting in the model because the convolution will blur the sharp discontinuities near faults and therefore make the faults look more realistic. To further improve the realism of the synthetic seismic image, we also add some random noise to the image as shown in Figure 1f. From this noisy image (Figure 1f), we crop a final training seismic image (Figure 2a) with the size of 128 × 128 × 128 to avoid the artifacts near the boundaries. Figure 2b shows the corresponding binary fault labeling image, in which the faults are labeled by ones at two pixels adjacent to the faults from the hanging wall and footwall sides.

By using this workflow, we randomly choose parameters of folding, faulting, wavelet peak frequency, and noise to obtain 200 pairs of 3D unique seismic images and corresponding fault labeling images. We can actually generate much more unique training data sets, but we found that 200 pairs of images are sufficient to train a pretty good neural network for fault segmentation. Using the same workflow, we also automatically generated 20 pairs of seismic and fault labeling images for the validation.

Data augmentation

Creating unique training seismic and fault labeling images, as discussed above, is crucial to successfully train a fault segmentation neural network. Data augmentation during the training is also helpful to increase the diversity of the data sets and to prevent the neural network from learning irrelevant patterns. We apply simple data augmentations including vertical flip and rotation around the vertical time or depth axis. To avoid interpolation and artifacts near boundaries, we rotate the seismic and fault labeling volumes by only three options of 90°, 180°, and 270°. Because our input seismic and fault labeling volumes are 128 × 128 × 128 cubes, the flip and rotation will preserve the image size without needing interpolation or extrapolation. Note that we do not want to rotate the seismic and fault volumes around the inline or crossline axis because it will yield vertical seismic structures and flat faults, which are geologically unrealistic.

Fault Segmentation By CNN

We consider 3D fault detection as an image segmentation problem of labeling ones on faults, whereas zeros elsewhere in a 3D seismic image. We achieve such fault segmentation by using a simplified version of U-Net, an end-to-end fully CNN, which was first proposed by Ronneberger et al. (2015) for biomedical image segmentation, and then it was widely used for many other image segmentation problems. In 3D seismic images, the distribution of fault samples and nonfault samples is typically highly imbalanced; therefore, we use a balanced binary cross-entropy loss to optimize the parameters of the network as discussed by Xie and Tu (2015).

CNN architecture

We started our research on fault segmentation by using the original U-Net architecture (Ronneberger et al., 2015), which turned out to be more complicated than necessary for our problem of fault detection. We reduce the convolutional layers and features at each layer to save memory and computation but still preserve good performance in fault detection.

The finally simplified U-Net that we use for 3D fault detection is shown in Figure 3, in which an input 3D seismic image is fed to a network that contains a contracting path (left side) and an expansive path (right side) as in the original U-Net architecture. In the left contracting path, each step contains two 3 × 3 × 3 convolutional layers followed by a ReLU activation and a 2 × 2 × 2 max pooling operation with stride 2 for downsampling. We double the number of features after each step. Every step in the right expansion path contains a 2 × 2 × 2 upsampling operation, a concatenation with features from the left contracting path, and two 3 × 3 × 3 convolutional layers followed by a ReLU activation. Different from the original U-Net architecture, we do not include a 2 × 2 × 2 “up-convolution” layer after each upsampling as in the original expansion path. The upsampling operation is implemented by using the function UpSampling3D defined in Keras (Chollet, 2015). The final output layer is a 1 × 1 × 1 convolutional layer with a sigmoid activation to map each 16C feature vector to a probability value in the output fault probability map, which has the same size as the input seismic image. This simplified U-Net architecture totally consists of 15 convolutional layers, reduced from 23 convolutional layers in the original U-Net architecture. The number of features at these convolutional layers is also significantly reduced from the original architecture.

Balanced cross-entropy loss

The following binary cross-entropy loss function is widely used in the binary segmentation of a common image:

where N denotes the number of pixels in the input 3D seismic image. The term yi represents the true binary labels and pi represents the prediction probabilities (0 < pi < 1) computed from the sigmoid activation in the last convolutional layer. Because the true labels yi are binary values (0 or 1), the first term measures the prediction errors at the image pixels labeled by ones, whereas the second term measures the prediction errors at the pixels labeled by zeros.

This loss function works well for binary segmentation of common images, in which the distribution of zero/nonzero samples is more or less balanced. This loss function, however, is not suitable to measure the errors of fault segmentation, in which more than 90% of the samples are nonfault samples (labeled by zeros), whereas the fault samples (labeled by ones) are very limited. If we train the neural network using this loss function, the network can easily converge to the wrong direction and make zero predictions everywhere because zero prediction is a good solution to this loss function in the fault segmentation problem.

To solve this problem, we use the following balanced cross-entropy loss function as discussed by Xie and Tu (2015):

where represents the ratio between nonfault pixels and the total image pixels, whereas 1 − β denotes the ratio of fault pixels in the 3D seismic image.

Training and validation

We train the CNN by using 200 pairs of synthetic 3D seismic and fault images that are automatically created as in Figures 1 and 2. The validation data set contains another 20 pairs of such synthetic seismic and fault images, which are not used in the training data set. Considering the amplitude values of different real seismic images can be much different from each other, we normalize all the training seismic images, each image is subtracted by its mean value and divided by its standard deviation.

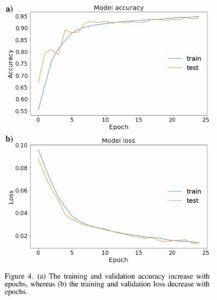
The size of each 3D seismic or fault image is 128 × 128 × 128. We choose this relatively small size because the memory of our GPU is limited to 12 GB. We would suggest to choose a larger size if the GPU memory is allowed. We feed the 3D seismic images to the neural network in batches and each batch contains four images, which consist of an original image and the same image rotated around the vertical time/depth axis by 90°, 180°, and 270°. We did not try a larger batch size, again, because of the GPU memory limitation. We use the Adam method (Kingma and Ba, 2014) to optimize the network parameters and set the learning rate to be 0.0001. We train the network with 25 epochs, and all the 200 training images are processed at each epoch. As shown in Figure 4, the training and validation accuracies gradually increase to 95%, whereas the training and validation loss converges to 0.01 after 25 epochs.

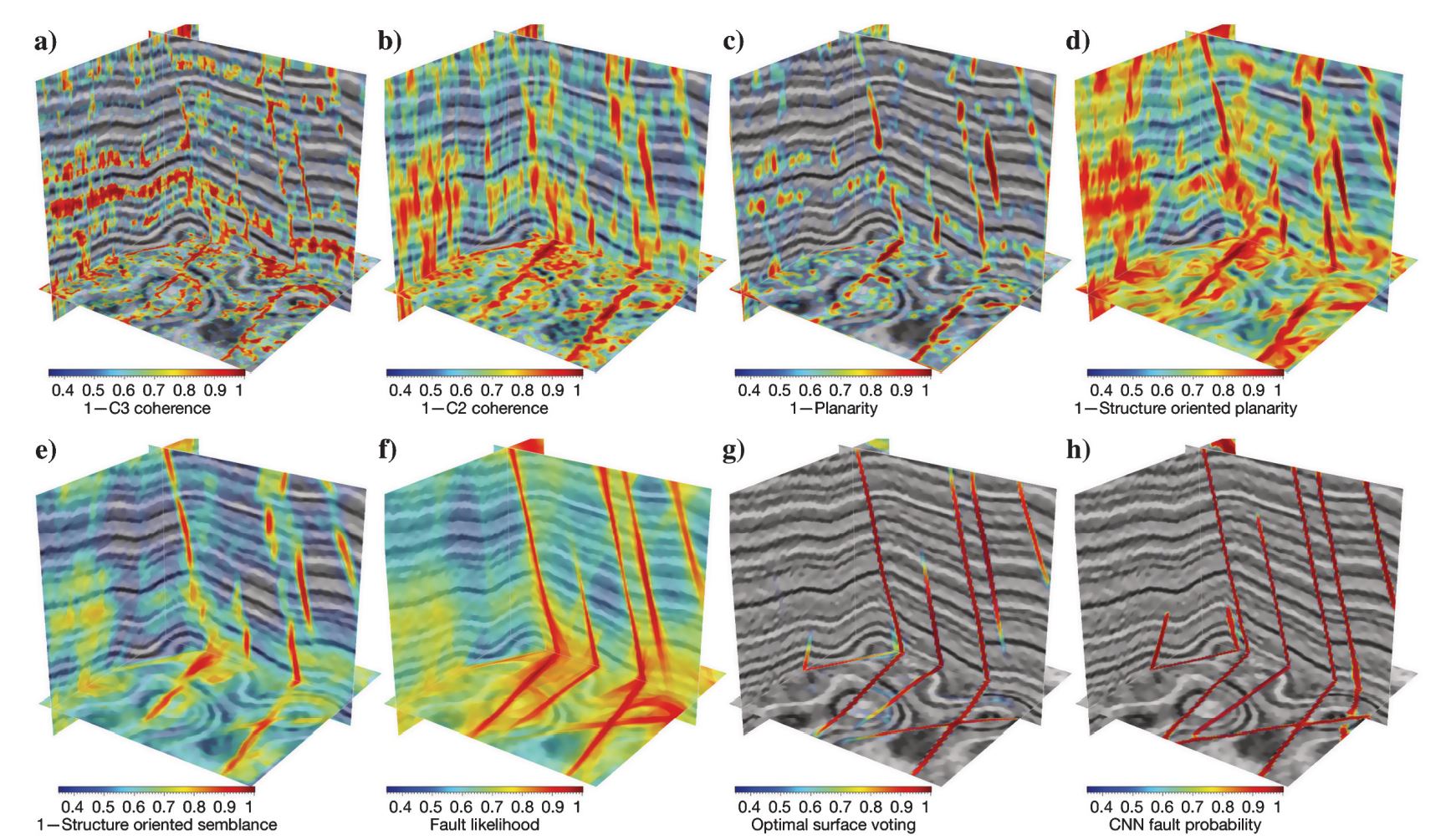
To verify the CNN model trained with 25 epochs, we apply this trained model together with another seven commonly used fault detection methods to the synthetic seismic volume (Figure 2a), which was not included in the training data sets. Figure 5a–5h shows all eight fault detection results that are, respectively, computed by using the methods of C3 (Gersztenkorn and Marfurt, 1999), C2 (Marfurt et al., 1999), planarity (Hale, 2009), structure-oriented linearity (Wu, 2017), structure-oriented semblance (Hale, 2009), fault likelihood (Hale, 2013; Wu and Hale, 2016), optimal surface voting (Wu and Fomel, 2018), and our CNN-based segmentation. The input for the optimal surface voting method is the planarity volume (Figure 5c), and the input for all the other methods is the amplitude volume (Figure 2a). Compared with the first five methods, the fault likelihood and optimal surface voting methods provide better fault detections in which the fault features are less noisy and can be more continuously tracked. Our CNN method achieves the best performance in computing an accurate, clean, and complete fault detection, which is most consistent with the true fault labeling shown in Figure 2b.

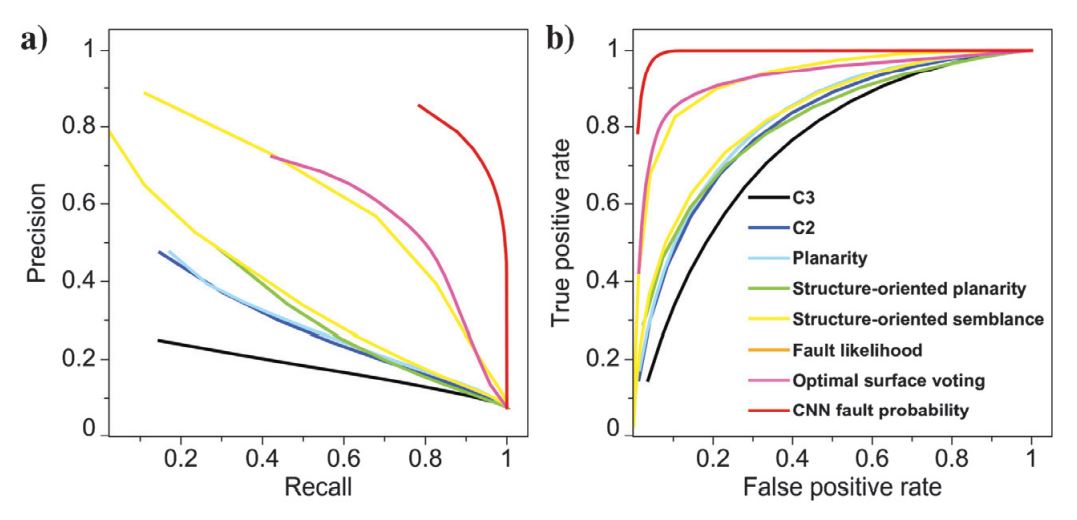
To quantitatively evaluate the fault detection methods, we further calculate the precision-recall (Martin et al., 2004) and receiver operating characteristic (ROC) (Provost et al., 1998) curves shown in Figure 6. From the precision-recall curves (Figure 6a), we can clearly observe that our CNN method (the red curve in Figure 6a) provides the highest precision for all choices of recall. The precisions of the fault likelihood (the orange curve in Figure 6a) and optimal surface voting (the magenta curve in Figure 6a) methods are relatively lower than the CNN method, but they are higher than the other five methods. The ROC curves in Figure 6b provide similar evaluations of the methods. In the next section, we will use the same CNN model (trained by only synthetic data sets) to four field seismic images that are acquired at different surveys. In this highly strict precision evaluation, the fault detections are expected to perfectly match the true fault labels with the thickness of only two samples. However, all of the methods should have higher precision if we consider that each fault is a thicker zone and all fault detections within the zone are good enough.

Applications

It might not be surprising that the CNN model, trained by synthetic data sets, works well to detect faults in a synthetic seismic image (Figure 5h) that is also created by using the same workflow for creating the training data sets. We further test the same CNN model on four field seismic images that are acquired at different surveys. To be consistent with the synthetic training seismic images, each of the field seismic images is subtracted by its mean value and divided by its standard deviation to obtain a consistently normalized image. We compare our fault prediction results with the thinned fault likelihood (Hale, 2013; Wu and Hale, 2016), which is a superior attribute (better than most of the conventional attributes [Figures 5 and 6]) for fault detection.

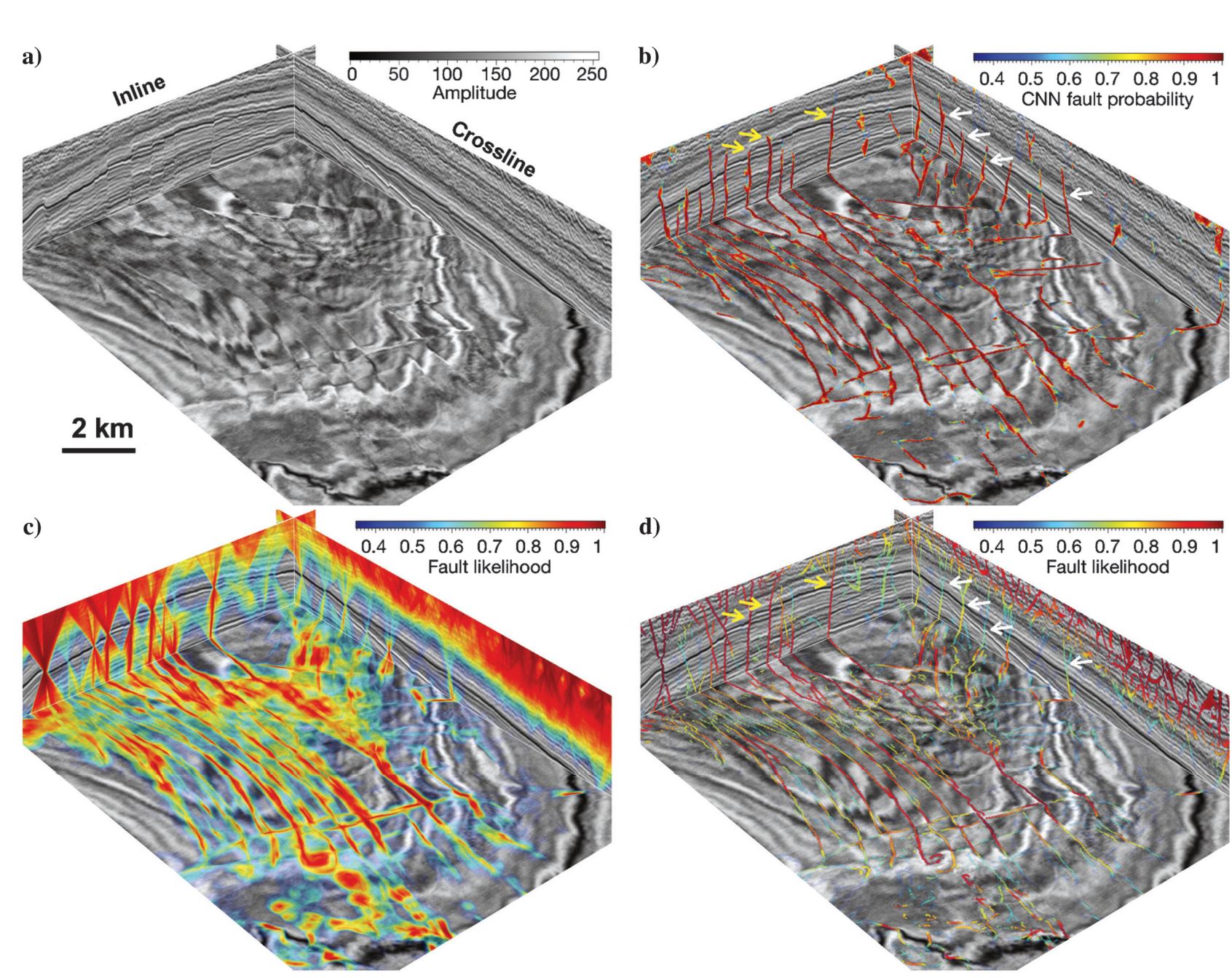
The first 3D seismic volume in Figure 7a is a subset (128 [vertical] × 384 [inline] × 512 [crossline] samples) extracted from the Netherlands off-shore F3 block seismic data, which is graciously provided by the Dutch government through TNO and dGB Earth Sciences. Multioriented faults are apparent within this 3D seismic volume. Figure 7b shows the fault probability image predicted by using the trained CNN model. The color in this fault image represents the fault probability, which is computed by the sigmoid activation in the last convolutional layer. Although trained by only synthetic data sets, this CNN model works pretty well to provide a clean and accurate prediction of faults in this field seismic image. In this CNN fault probability image, most fault features have very high probabilities (close to 1) and only very limited noisy features are observed. Although we added only planar faults in the training data sets, the networks actually learn to detect curved faults in the field seismic image as shown on the time slice in Figure 7b. Figure 7c and 7d, respectively, shows the fault likelihood attribute (Hale, 2013; Wu and Hale, 2016) before and after thinning. The thinned fault likelihood (Figure 7d) works fine to highlight the faults within this seismic image. However, a lot of more noisy features are observed than in the CNN fault probability image (Figure 7b). In addition, as denoted by the yellow arrows on the inline slice (Figure 7d), the fault-oriented smoothing in calculating the fault likelihood actually extends the fault features beyond the top of true faults. In addition, the fault likelihood is computed from the semblance/coherence of seismic reflections, which can be sensitive to noisy reflections (the red features on the crossline in Figure 7d) but insensitive to the faults with small fault displacements (like those faults denoted by white arrows in Figure 7d). However, the trained CNN model is more robust to noise and can better measure the probability of faults with small displacements.

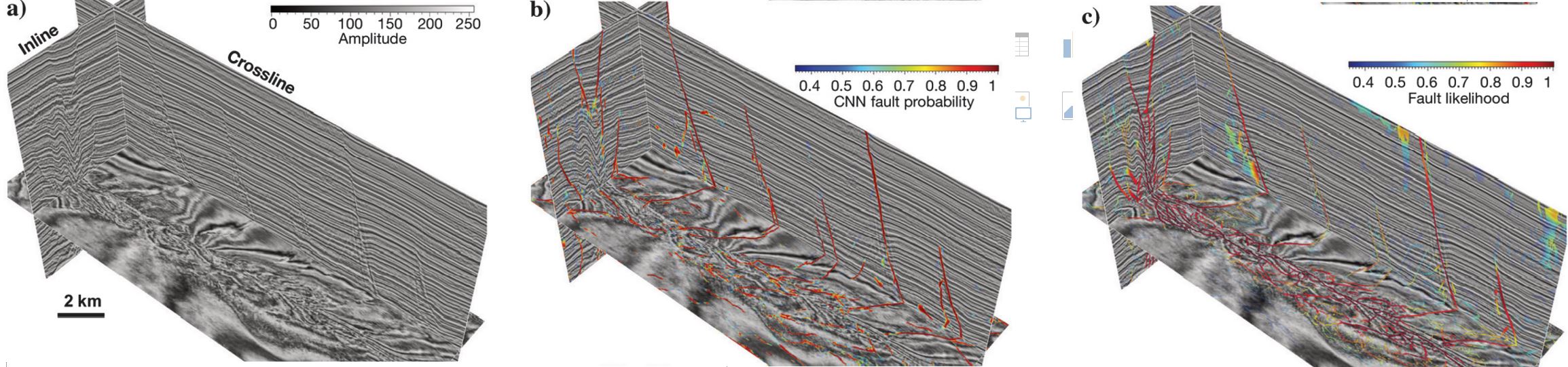
The second 3D seismic image shown in Figure 8a is graciously provided by Clyde Petroleum Plc. through Paradigm. Different from the previous synthetic and field examples, the faults in this seismic image are not apparent as sharp reflection discontinuities. Instead, the faults are imaged like reflections in this 3D seismic image as shown in Figure 8a. However, the CNN model still works pretty well to detect the faults shown in Figure 8b, which means that the network wisely learned to predict faults by not detecting sharp discontinuities or edges. Figure 8c shows the thinned fault likelihoods that are noisier than the CNN fault probabilities as shown on the horizontal slice.

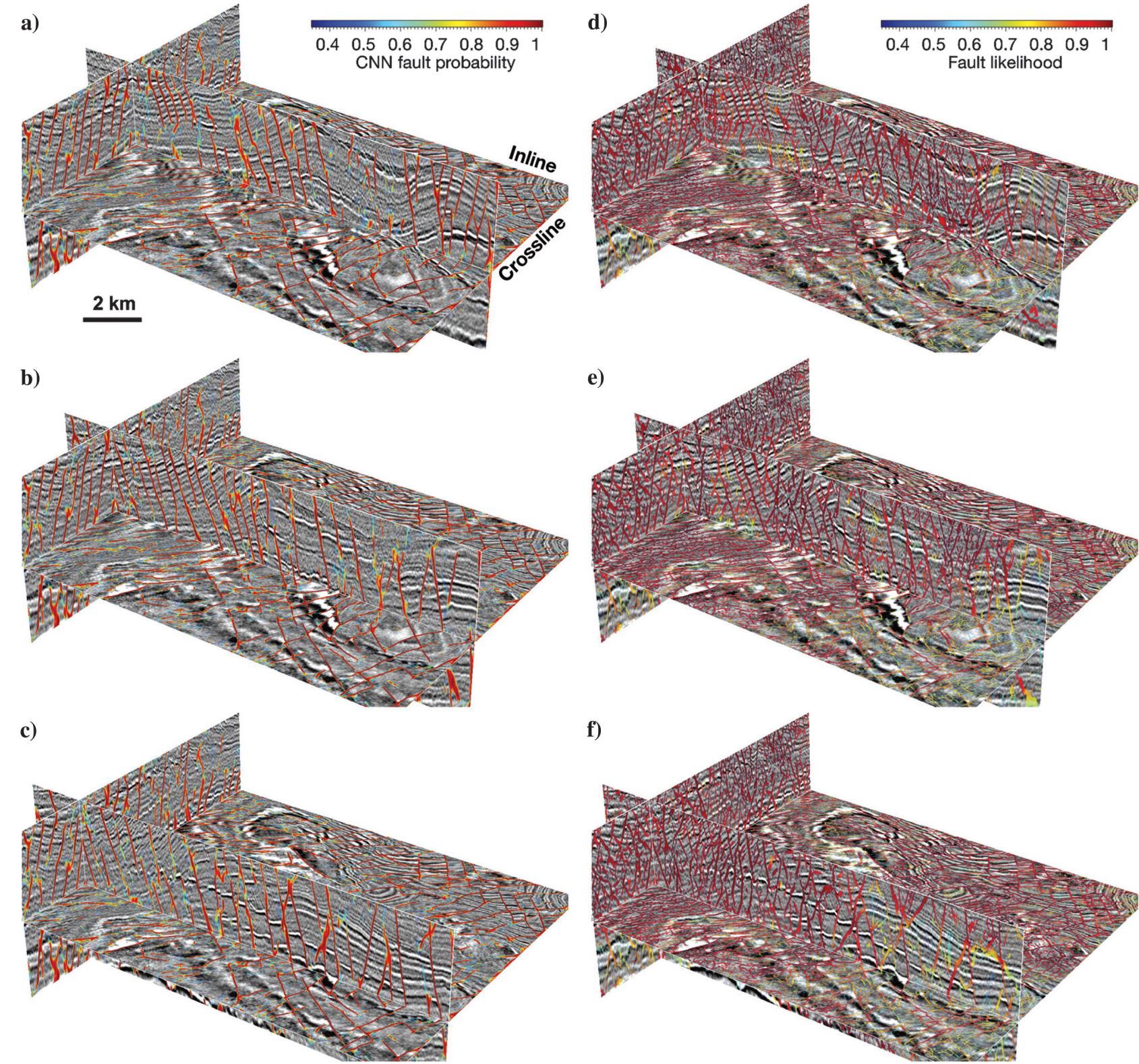
The third 3D seismic image shown in Figure 9 is a subset (210 [vertical] × 600 [inline] × 825 [crossline] samples) extracted from a larger seismic reflection volume that is acquired across the Costa Rica margin, northwest of the Osa Peninsula to image the fault properties in the subduction zone. Multiple sets of closely spaced faults are apparent in this 3D seismic volume as discussed by Bangs et al. (2015). The fault detection in this example is more challenging than the previous ones because the faults are very close to each other, the reflection structures are not well-imaged, and the image is pretty noisy. Figure 9a–9c shows the CNN fault probabilities at different slices. We observe that most faults are clearly labeled in this CNN fault probability images, and these faults can be continuously tracked by following the probability features. Multiple sets of faults striking in different directions can be clearly observed on the horizontal slice in these CNN fault probability images. Figure 9d–9f shows the thinned fault likelihoods at the same slices, which can detect most faults, but the fault features are much noisier than the CNN fault probabilities. In addition, many of the faults are mislabeled, especially in areas where the seismic structures are noisy.

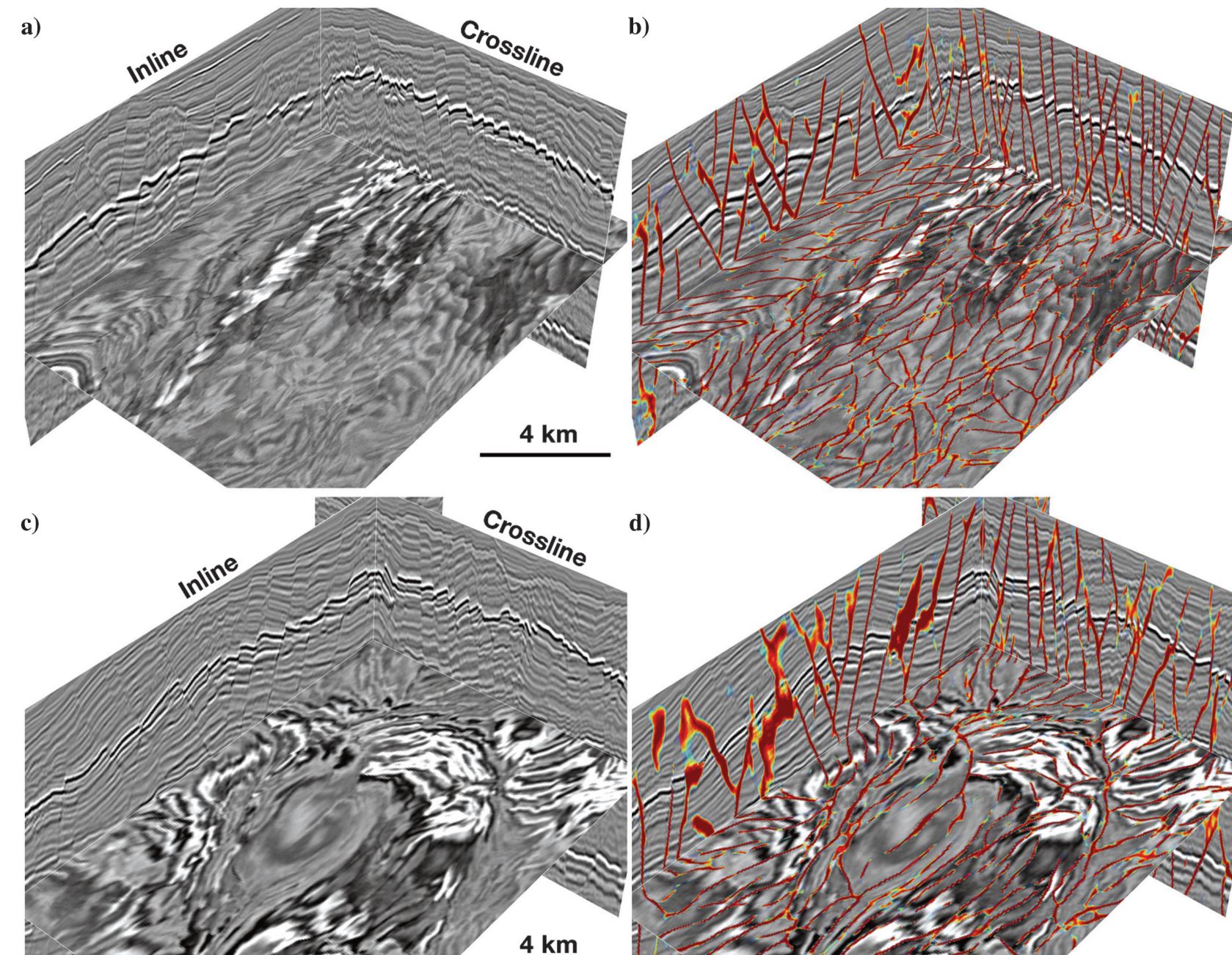
Figure 10 shows the fourth larger seismic volume (450 [vertical] × 1950 [inline] × 1200 [crossline] samples) that is acquired at the Campos Basin, offshore Brazil. This image shows that the sediments are heavily faulted due to the salt bodies at the bottom of the volume. The CNN fault probabilities shown in Figure 10a and 10b clearly and accurately label numerous closely spaced faults in this seismic volume. The faulting patterns are clearly visible on the time slices of the CNN fault probability image. To be able to better visualize the fault detection in this example, we further display two subvolumes of seismic amplitude and CNN fault probabilities (Figure 11b and 11d), in which most of the faults are clearly and accurately labeled except some subtle faults. The horizontal slices in Figure 11b and 11d, respectively, display clear patterns of polygonal and radial faults that may be associated with salt diapirs (Rowan et al., 1999; Carruthers, 2012).

In addition to the above field examples, we also applied the same trained CNN model to two other 3D seismic images Kerry-3D and Opunake-3D, which are provided on the SEG Wiki website. The fault segmentation results are clean and accurate as shown in the SEG Wiki website (Wu, 2018a, 2018b, 2019).

In summary, although the CNN model is trained by using only 200 synthetic seismic images, it works pretty well to detect faults in 3D field seismic volumes that are recorded at totally different surveys. In addition, the 3D fault prediction using the trained CNN model is highly efficient. By using one TITAN Xp GPU, computing the large CNN fault probability volume (450 [vertical] × 1950 [inline] × 1200 [crossline] samples) in Figure 10 takes less than 3 min. Computing fault likelihoods for the same volume, however, required approximately 1.5 h when using a workstation with 32 cores.

In our training and validating data sets, we avoid including thrust and listric faults with low dip angles. These faults often appear strong reflection features in a seismic image other than reflection discontinuities as the faults discussed in this paper. Therefore, all the conventional fault detection methods, based on measuring reflection discontinuity or continuity, often fail to detect the thrust and listric faults. However, our CNN-based method has potential to successfully detect these faults by training another specific model, which is actually what we will focus on in future research.

Conclusion

We have discussed an end-to-end CNN to efficiently detect faults from 3D seismic images, in which the fault detection is considered as a binary segmentation problem. This neural network is simplified from the originally more complicated U-Net to save GPU memory and computational time (for training and prediction) but still reserve the high performance for fault detection. Because the distribution of fault and nonfault samples is heavily biased, we use a balanced loss function to optimize the CNN model parameters. We train the neural network by using only 200 pairs of 3D synthetic seismic and fault volumes, which are all automatically generated by randomly adding folding, faulting, and noise in the volumes. Although trained by using only synthetic data sets, the neural network can accurately detect faults from 3D field seismic volumes that are acquired at totally different surveys. Although we add only planar faults in the training data sets, the network actually learns to detect curved faults in the field seismic images.

Acknowledgement

This research is financially supported by the sponsors of the Texas Consortium for Computation Seismology (TCCS). The 1st, 3rd and 4th authors gratefully acknowledge the support of NVIDIA Corporation with the donation of the Titan Xp GPU used for this research.